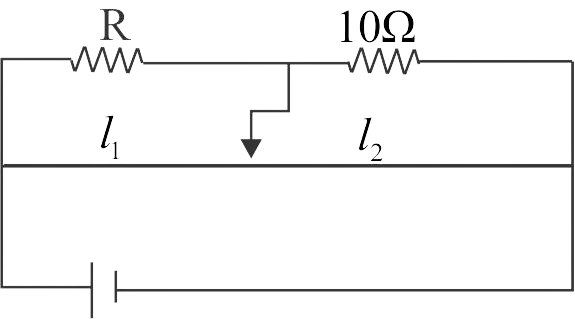
357274 A resistance wire connected in the left gap of a metre bridge balances a \(10\Omega \) resistance in the right gap at a point which divides the bridge wire in the ratio 3:2. If the length of the resistance wire is 1.5 \(m\), then the length of \(1\Omega \) of the resistance wire is:
357275
In a meter bridge as shown in the figure it is given that resistance \(Y = 12.5\,\Omega \) and that the balance is obtained at a distance 39.5 \(cm\) from end \(A\) (by Jockey \(J\)). After interchanging the resistances \(X\) and \(Y\) a new balance point is found at a distance \({l_2}\) from end \(A\). What are the values of \(X\) and \({l_2}\)?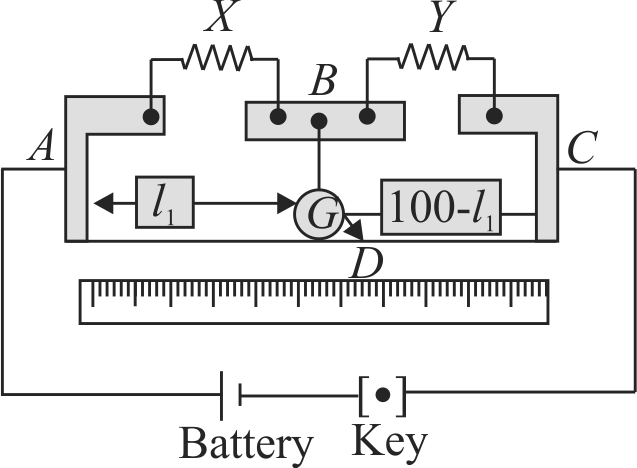
357276
In a metre bridge experiment, resistances are connected as shown in figure. The balancing length \({l_1}\) is 55 \(cm\). Now an unknown resistance \(x\) is connected in series with \(P\left( {P = 3\Omega } \right)\) and the new balancing length is found to be 75 \(cm\). The value of \(x\) is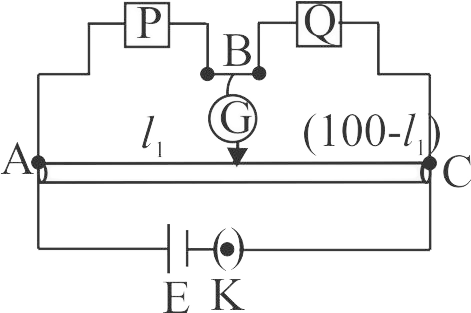
357274 A resistance wire connected in the left gap of a metre bridge balances a \(10\Omega \) resistance in the right gap at a point which divides the bridge wire in the ratio 3:2. If the length of the resistance wire is 1.5 \(m\), then the length of \(1\Omega \) of the resistance wire is:
357275
In a meter bridge as shown in the figure it is given that resistance \(Y = 12.5\,\Omega \) and that the balance is obtained at a distance 39.5 \(cm\) from end \(A\) (by Jockey \(J\)). After interchanging the resistances \(X\) and \(Y\) a new balance point is found at a distance \({l_2}\) from end \(A\). What are the values of \(X\) and \({l_2}\)?
357276
In a metre bridge experiment, resistances are connected as shown in figure. The balancing length \({l_1}\) is 55 \(cm\). Now an unknown resistance \(x\) is connected in series with \(P\left( {P = 3\Omega } \right)\) and the new balancing length is found to be 75 \(cm\). The value of \(x\) is
357274 A resistance wire connected in the left gap of a metre bridge balances a \(10\Omega \) resistance in the right gap at a point which divides the bridge wire in the ratio 3:2. If the length of the resistance wire is 1.5 \(m\), then the length of \(1\Omega \) of the resistance wire is:
357275
In a meter bridge as shown in the figure it is given that resistance \(Y = 12.5\,\Omega \) and that the balance is obtained at a distance 39.5 \(cm\) from end \(A\) (by Jockey \(J\)). After interchanging the resistances \(X\) and \(Y\) a new balance point is found at a distance \({l_2}\) from end \(A\). What are the values of \(X\) and \({l_2}\)?
357276
In a metre bridge experiment, resistances are connected as shown in figure. The balancing length \({l_1}\) is 55 \(cm\). Now an unknown resistance \(x\) is connected in series with \(P\left( {P = 3\Omega } \right)\) and the new balancing length is found to be 75 \(cm\). The value of \(x\) is
357274 A resistance wire connected in the left gap of a metre bridge balances a \(10\Omega \) resistance in the right gap at a point which divides the bridge wire in the ratio 3:2. If the length of the resistance wire is 1.5 \(m\), then the length of \(1\Omega \) of the resistance wire is:
357275
In a meter bridge as shown in the figure it is given that resistance \(Y = 12.5\,\Omega \) and that the balance is obtained at a distance 39.5 \(cm\) from end \(A\) (by Jockey \(J\)). After interchanging the resistances \(X\) and \(Y\) a new balance point is found at a distance \({l_2}\) from end \(A\). What are the values of \(X\) and \({l_2}\)?
357276
In a metre bridge experiment, resistances are connected as shown in figure. The balancing length \({l_1}\) is 55 \(cm\). Now an unknown resistance \(x\) is connected in series with \(P\left( {P = 3\Omega } \right)\) and the new balancing length is found to be 75 \(cm\). The value of \(x\) is