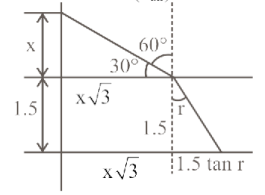
282087 A pole is vertically submerged in swimming pool, such that is gives a length of shadow 2.15 $m$ within water when sunlight is incident at an angle of $30^{\circ}$ with the surface of water. If swimming pool is filled to a height of $1.5 \mathrm{~m}$, then the height of the pole above the water surface in centimeters is $\left(n_w=4 / 3\right)$

Ans. (50) : Given data,
Shadow length of pole $=2.15 \mathrm{~m}$
Incident angle $=30^{\circ}$
height of water in swimming pool $=1.5 \mathrm{~m}$
Refractive index of water $\left(n_w\right)=4 / 3$
Refractive index of air $\left(\mathrm{n}_{\text {air }}\right)=1$
From snell's law,
$\begin{aligned}
1 \sin 60^{\circ}=\frac{4}{3} \sin r \\
\sin r=\frac{3 \sqrt{3}}{8} \text { this gives } \tan r=\frac{3 \sqrt{3}}{\sqrt{37}}
\end{aligned}$
From the diagram,
$\begin{aligned}
x \sqrt{3}+1.5 \tan r=2.15 \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x=\frac{2.15-1.281}{\sqrt{3}} \\
x=0.50 \mathrm{~m} \\
x=50 \mathrm{~cm}
\end{aligned}$

282088 A monochromatic light wave with wavelength $\lambda_1$ and frequency $v_1$ in air enters another medium. If the angle of incidence and angle of refraction at the interface are $45^{\circ}$ and $30^{\circ}$ respectively, then the wavelength $\lambda_2$ and frequency $v_2$ of the refracted wave are :

282089 Given below are two statement:
Statement I : If the Brewster's angle for the light propagating from air to glass is $\theta_B$, then the Brewster's angle for the light propagating
from glass to air is $\frac{\pi}{2}-\theta_B$.
Statement II: The Brewster's angle for the light propagating from glass to air is $\tan ^{-1}\left(\mu_{\mathrm{g}}\right)$ where $\mu_{\mathrm{g}}$ is the refractive index of glass.
In the light of the above statement, choose the correct answer from the option given below:

282090 The refractive index of crown glass is close to $3 / 2$. If the speed of light in the crown glass will be close to

282087 A pole is vertically submerged in swimming pool, such that is gives a length of shadow 2.15 $m$ within water when sunlight is incident at an angle of $30^{\circ}$ with the surface of water. If swimming pool is filled to a height of $1.5 \mathrm{~m}$, then the height of the pole above the water surface in centimeters is $\left(n_w=4 / 3\right)$

Ans. (50) : Given data,
Shadow length of pole $=2.15 \mathrm{~m}$
Incident angle $=30^{\circ}$
height of water in swimming pool $=1.5 \mathrm{~m}$
Refractive index of water $\left(n_w\right)=4 / 3$
Refractive index of air $\left(\mathrm{n}_{\text {air }}\right)=1$
From snell's law,
$\begin{aligned}
1 \sin 60^{\circ}=\frac{4}{3} \sin r \\
\sin r=\frac{3 \sqrt{3}}{8} \text { this gives } \tan r=\frac{3 \sqrt{3}}{\sqrt{37}}
\end{aligned}$
From the diagram,
$\begin{aligned}
x \sqrt{3}+1.5 \tan r=2.15 \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x=\frac{2.15-1.281}{\sqrt{3}} \\
x=0.50 \mathrm{~m} \\
x=50 \mathrm{~cm}
\end{aligned}$

282088 A monochromatic light wave with wavelength $\lambda_1$ and frequency $v_1$ in air enters another medium. If the angle of incidence and angle of refraction at the interface are $45^{\circ}$ and $30^{\circ}$ respectively, then the wavelength $\lambda_2$ and frequency $v_2$ of the refracted wave are :

282089 Given below are two statement:
Statement I : If the Brewster's angle for the light propagating from air to glass is $\theta_B$, then the Brewster's angle for the light propagating
from glass to air is $\frac{\pi}{2}-\theta_B$.
Statement II: The Brewster's angle for the light propagating from glass to air is $\tan ^{-1}\left(\mu_{\mathrm{g}}\right)$ where $\mu_{\mathrm{g}}$ is the refractive index of glass.
In the light of the above statement, choose the correct answer from the option given below:

282090 The refractive index of crown glass is close to $3 / 2$. If the speed of light in the crown glass will be close to

282087 A pole is vertically submerged in swimming pool, such that is gives a length of shadow 2.15 $m$ within water when sunlight is incident at an angle of $30^{\circ}$ with the surface of water. If swimming pool is filled to a height of $1.5 \mathrm{~m}$, then the height of the pole above the water surface in centimeters is $\left(n_w=4 / 3\right)$

Ans. (50) : Given data,
Shadow length of pole $=2.15 \mathrm{~m}$
Incident angle $=30^{\circ}$
height of water in swimming pool $=1.5 \mathrm{~m}$
Refractive index of water $\left(n_w\right)=4 / 3$
Refractive index of air $\left(\mathrm{n}_{\text {air }}\right)=1$
From snell's law,
$\begin{aligned}
1 \sin 60^{\circ}=\frac{4}{3} \sin r \\
\sin r=\frac{3 \sqrt{3}}{8} \text { this gives } \tan r=\frac{3 \sqrt{3}}{\sqrt{37}}
\end{aligned}$
From the diagram,
$\begin{aligned}
x \sqrt{3}+1.5 \tan r=2.15 \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x=\frac{2.15-1.281}{\sqrt{3}} \\
x=0.50 \mathrm{~m} \\
x=50 \mathrm{~cm}
\end{aligned}$

282088 A monochromatic light wave with wavelength $\lambda_1$ and frequency $v_1$ in air enters another medium. If the angle of incidence and angle of refraction at the interface are $45^{\circ}$ and $30^{\circ}$ respectively, then the wavelength $\lambda_2$ and frequency $v_2$ of the refracted wave are :

282089 Given below are two statement:
Statement I : If the Brewster's angle for the light propagating from air to glass is $\theta_B$, then the Brewster's angle for the light propagating
from glass to air is $\frac{\pi}{2}-\theta_B$.
Statement II: The Brewster's angle for the light propagating from glass to air is $\tan ^{-1}\left(\mu_{\mathrm{g}}\right)$ where $\mu_{\mathrm{g}}$ is the refractive index of glass.
In the light of the above statement, choose the correct answer from the option given below:

282090 The refractive index of crown glass is close to $3 / 2$. If the speed of light in the crown glass will be close to

282087 A pole is vertically submerged in swimming pool, such that is gives a length of shadow 2.15 $m$ within water when sunlight is incident at an angle of $30^{\circ}$ with the surface of water. If swimming pool is filled to a height of $1.5 \mathrm{~m}$, then the height of the pole above the water surface in centimeters is $\left(n_w=4 / 3\right)$

Ans. (50) : Given data,
Shadow length of pole $=2.15 \mathrm{~m}$
Incident angle $=30^{\circ}$
height of water in swimming pool $=1.5 \mathrm{~m}$
Refractive index of water $\left(n_w\right)=4 / 3$
Refractive index of air $\left(\mathrm{n}_{\text {air }}\right)=1$
From snell's law,
$\begin{aligned}
1 \sin 60^{\circ}=\frac{4}{3} \sin r \\
\sin r=\frac{3 \sqrt{3}}{8} \text { this gives } \tan r=\frac{3 \sqrt{3}}{\sqrt{37}}
\end{aligned}$
From the diagram,
$\begin{aligned}
x \sqrt{3}+1.5 \tan r=2.15 \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x \sqrt{3}=2.15-1.5 \times \frac{3 \sqrt{3}}{\sqrt{37}} \\
x=\frac{2.15-1.281}{\sqrt{3}} \\
x=0.50 \mathrm{~m} \\
x=50 \mathrm{~cm}
\end{aligned}$

282088 A monochromatic light wave with wavelength $\lambda_1$ and frequency $v_1$ in air enters another medium. If the angle of incidence and angle of refraction at the interface are $45^{\circ}$ and $30^{\circ}$ respectively, then the wavelength $\lambda_2$ and frequency $v_2$ of the refracted wave are :

282089 Given below are two statement:
Statement I : If the Brewster's angle for the light propagating from air to glass is $\theta_B$, then the Brewster's angle for the light propagating
from glass to air is $\frac{\pi}{2}-\theta_B$.
Statement II: The Brewster's angle for the light propagating from glass to air is $\tan ^{-1}\left(\mu_{\mathrm{g}}\right)$ where $\mu_{\mathrm{g}}$ is the refractive index of glass.
In the light of the above statement, choose the correct answer from the option given below:

282090 The refractive index of crown glass is close to $3 / 2$. If the speed of light in the crown glass will be close to