282041
A linear object of height $10 \mathrm{~cm}$ is kept in front of a concave mirror of radius of curature 15 $\mathrm{cm}$, at a distance of $10 \mathrm{~cm}$. The image formed is:
1 magnified and erect
2 magnified and inverted
3 diminished and erect
4 diminished and inverted
Explanation:
B: Given, Object height $\left(\mathrm{h}_{\mathrm{o}}\right)=10 \mathrm{~cm}$
Radius of curvature of mirror $(\mathrm{R})=-15 \mathrm{~cm}$
Focus of mirror $(f)=-\frac{15}{2} \mathrm{~cm}$
Object distance from the mirror $(\mathrm{u})=-10 \mathrm{~cm}$
By using mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{\frac{15}{2}}=-\frac{1}{10}+\frac{1}{\mathrm{~V}} \\
\frac{1}{\mathrm{~V}}=\frac{1}{10}-\frac{2}{15} \\
\frac{1}{\mathrm{~V}}=\frac{3-4}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
We know that,
$\begin{array}{r}
\text { Magnification }(\mathrm{m})=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}} \\
\therefore \quad-\frac{(-30)}{(-10)}=\frac{\mathrm{h}_{\mathrm{i}}}{10} \\
\mathrm{~h}_{\mathrm{i}}=-30 \mathrm{~cm}
\end{array}$
Hence, images are magnified and inverted.
Karnataka CET-2017
Ray Optics
282042
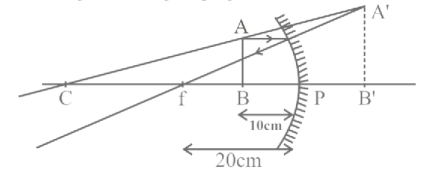
If an object is placed $10 \mathrm{~cm}$ in front of a concave mirror of focal length $20 \mathrm{~cm}$, the image will be
1 diminished, upright, virtual
2 enlarged, upright, virtual
3 diminished, inverted, real
4 enlarged, upright, real
Explanation:
B: Given, object distance $=10 \mathrm{~cm}$
Focal length $=20 \mathrm{~cm}$
From the above value, it is clear that, object is placed between focal length and pole.
Hence, image is enlarge, upright and virtual
CG PET- 2007
Ray Optics
282043
A point object is placed at a distance of $10 \mathrm{~cm}$ and its real image is formed at a distance of $\mathbf{2 0}$ $\mathrm{cm}$ from a concave mirror. If the object is moved by $0.1 \mathrm{~cm}$ towards the mirror, the image will shift by about
1 $0.4 \mathrm{~cm}$ away from the mirror
2 $0.4 \mathrm{~cm}$ towards the mirror
3 $0.8 \mathrm{~cm}$ away from the mirror
4 $0.8 \mathrm{~cm}$ towards the mirror
Explanation:
A: Given, object placed (u) $=-10 \mathrm{~cm}$
Image formed at distance $(\mathrm{v})=-20 \mathrm{~cm}$ (real)
For focal length of concave mirror,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{10}-\frac{1}{20} \\
\frac{1}{\mathrm{f}}=\frac{-1-2}{20}=\frac{-3}{20} \\
\mathrm{f}=-\frac{20}{3}
\end{aligned}$
When object move $0.1 \mathrm{~cm}$ toward the mirror then new position of object -
$\mathrm{u}=10-0.1=9.9 \mathrm{~cm}$
Then, new position of image -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}^{\prime}}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{-\left(\frac{20}{3}\right)}=\frac{1}{-9.9}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-3}{20}+\frac{1}{9.9} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-29.7+20}{20 \times 9.9}
\end{aligned}$
$\begin{aligned}
\mathrm{v}^{\prime} & =\frac{20 \times 9.9}{-9.7} \\
\mathrm{v}^{\prime} & =\frac{-198}{9.7} \\
\mathrm{v}^{\prime} & =-20.4 \mathrm{~cm}
\end{aligned}$
Image shifted $=20.4-20=0.4 \mathrm{~cm}$
Hence, image shifted $0.4 \mathrm{~cm}$ away from the mirror.
CG PET- 2005
Ray Optics
282044
Radius of curvature of concave mirror is $40 \mathrm{~cm}$ and the size of image of real is twice as that of object, then the object distance is
1 $60 \mathrm{~cm}$
2 $20 \mathrm{~cm}$
3 $40 \mathrm{~cm}$
4 $30 \mathrm{~cm}$
Explanation:
D: Given, radius of curvature (R) $=-40 \mathrm{~cm}$
Then, focal length $=-\frac{40}{2}=-20 \mathrm{~cm}$
Magnification $=-2$ (for real image)
$\begin{aligned}
-2=\frac{-\mathrm{v}}{\mathrm{u}} \\
\mathrm{v}=2 \mathrm{u}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{20}=\frac{1}{\mathrm{u}}+\frac{1}{2 \mathrm{u}} \\
-\frac{1}{20}=\frac{3}{2 \mathrm{u}} \\
\mathrm{u}=-30 \mathrm{~cm}
\end{aligned}$
Hence, distance of object is $30 \mathrm{~cm}$.
CG PET- 2007
Ray Optics
282045
A point object is moving on the principal axis of a concave mirror of focal length $24 \mathrm{~cm}$ towards the mirror. When it is at a distance of $60 \mathrm{~cm}$ from the mirror, its velocity is $9 \mathrm{~cm} / \mathrm{s}$. What is the velocity of the image at that instant?
1 $5 \mathrm{~cm} / \mathrm{s}$ towards the mirror
2 $4 \mathrm{~cm} / \mathrm{s}$ towards the mirror
3 $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror
4 $9 \mathrm{~cm} / \mathrm{s}$ away from the mirror
Explanation:
C: Given, focal length (f) $=-24 \mathrm{~cm}$
Object distance $(\mathrm{u})=-60 \mathrm{~cm}$
And, initial velocity of object $\left(\mathrm{u}_{\mathrm{i}}\right)=9 \mathrm{~cm} / \mathrm{s}$
Final velocity of object $\left(\mathrm{v}_{\mathrm{f}}\right)=$ ?
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{(-24)}=\frac{1}{(-60)}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{v}}=\frac{1}{60}-\frac{1}{24} \\
\frac{1}{\mathrm{~V}}=\frac{2-5}{120} \\
\mathrm{v}=-\frac{120}{3} \\
\mathrm{v}=-40 \mathrm{~cm}
\end{aligned}$
And, $\quad \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}$
Now, differentiating the above equation with respect to time -
$\begin{aligned}
0=-\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}=-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^2}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}} \quad\left(\because \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{v}_{\mathrm{f}}\right) \\
\mathrm{v}_{\mathrm{f}}=-\left(\frac{-40}{-60}\right)^2 \times \mathrm{u}_{\mathrm{i}} \\
\mathrm{v}_{\mathrm{f}}=-\frac{4}{9} \times 9 \\
\mathrm{v}_{\mathrm{f}}=-4 \mathrm{~cm} / \mathrm{s}
\end{aligned}$
Hence, velocity of image is $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror.
282041
A linear object of height $10 \mathrm{~cm}$ is kept in front of a concave mirror of radius of curature 15 $\mathrm{cm}$, at a distance of $10 \mathrm{~cm}$. The image formed is:
1 magnified and erect
2 magnified and inverted
3 diminished and erect
4 diminished and inverted
Explanation:
B: Given, Object height $\left(\mathrm{h}_{\mathrm{o}}\right)=10 \mathrm{~cm}$
Radius of curvature of mirror $(\mathrm{R})=-15 \mathrm{~cm}$
Focus of mirror $(f)=-\frac{15}{2} \mathrm{~cm}$
Object distance from the mirror $(\mathrm{u})=-10 \mathrm{~cm}$
By using mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{\frac{15}{2}}=-\frac{1}{10}+\frac{1}{\mathrm{~V}} \\
\frac{1}{\mathrm{~V}}=\frac{1}{10}-\frac{2}{15} \\
\frac{1}{\mathrm{~V}}=\frac{3-4}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
We know that,
$\begin{array}{r}
\text { Magnification }(\mathrm{m})=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}} \\
\therefore \quad-\frac{(-30)}{(-10)}=\frac{\mathrm{h}_{\mathrm{i}}}{10} \\
\mathrm{~h}_{\mathrm{i}}=-30 \mathrm{~cm}
\end{array}$
Hence, images are magnified and inverted.
Karnataka CET-2017
Ray Optics
282042
If an object is placed $10 \mathrm{~cm}$ in front of a concave mirror of focal length $20 \mathrm{~cm}$, the image will be
1 diminished, upright, virtual
2 enlarged, upright, virtual
3 diminished, inverted, real
4 enlarged, upright, real
Explanation:
B: Given, object distance $=10 \mathrm{~cm}$
Focal length $=20 \mathrm{~cm}$
From the above value, it is clear that, object is placed between focal length and pole.
Hence, image is enlarge, upright and virtual

CG PET- 2007
Ray Optics
282043
A point object is placed at a distance of $10 \mathrm{~cm}$ and its real image is formed at a distance of $\mathbf{2 0}$ $\mathrm{cm}$ from a concave mirror. If the object is moved by $0.1 \mathrm{~cm}$ towards the mirror, the image will shift by about
1 $0.4 \mathrm{~cm}$ away from the mirror
2 $0.4 \mathrm{~cm}$ towards the mirror
3 $0.8 \mathrm{~cm}$ away from the mirror
4 $0.8 \mathrm{~cm}$ towards the mirror
Explanation:
A: Given, object placed (u) $=-10 \mathrm{~cm}$
Image formed at distance $(\mathrm{v})=-20 \mathrm{~cm}$ (real)
For focal length of concave mirror,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{10}-\frac{1}{20} \\
\frac{1}{\mathrm{f}}=\frac{-1-2}{20}=\frac{-3}{20} \\
\mathrm{f}=-\frac{20}{3}
\end{aligned}$
When object move $0.1 \mathrm{~cm}$ toward the mirror then new position of object -
$\mathrm{u}=10-0.1=9.9 \mathrm{~cm}$
Then, new position of image -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}^{\prime}}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{-\left(\frac{20}{3}\right)}=\frac{1}{-9.9}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-3}{20}+\frac{1}{9.9} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-29.7+20}{20 \times 9.9}
\end{aligned}$
$\begin{aligned}
\mathrm{v}^{\prime} & =\frac{20 \times 9.9}{-9.7} \\
\mathrm{v}^{\prime} & =\frac{-198}{9.7} \\
\mathrm{v}^{\prime} & =-20.4 \mathrm{~cm}
\end{aligned}$
Image shifted $=20.4-20=0.4 \mathrm{~cm}$
Hence, image shifted $0.4 \mathrm{~cm}$ away from the mirror.
CG PET- 2005
Ray Optics
282044
Radius of curvature of concave mirror is $40 \mathrm{~cm}$ and the size of image of real is twice as that of object, then the object distance is
1 $60 \mathrm{~cm}$
2 $20 \mathrm{~cm}$
3 $40 \mathrm{~cm}$
4 $30 \mathrm{~cm}$
Explanation:
D: Given, radius of curvature (R) $=-40 \mathrm{~cm}$
Then, focal length $=-\frac{40}{2}=-20 \mathrm{~cm}$
Magnification $=-2$ (for real image)
$\begin{aligned}
-2=\frac{-\mathrm{v}}{\mathrm{u}} \\
\mathrm{v}=2 \mathrm{u}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{20}=\frac{1}{\mathrm{u}}+\frac{1}{2 \mathrm{u}} \\
-\frac{1}{20}=\frac{3}{2 \mathrm{u}} \\
\mathrm{u}=-30 \mathrm{~cm}
\end{aligned}$
Hence, distance of object is $30 \mathrm{~cm}$.
CG PET- 2007
Ray Optics
282045
A point object is moving on the principal axis of a concave mirror of focal length $24 \mathrm{~cm}$ towards the mirror. When it is at a distance of $60 \mathrm{~cm}$ from the mirror, its velocity is $9 \mathrm{~cm} / \mathrm{s}$. What is the velocity of the image at that instant?
1 $5 \mathrm{~cm} / \mathrm{s}$ towards the mirror
2 $4 \mathrm{~cm} / \mathrm{s}$ towards the mirror
3 $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror
4 $9 \mathrm{~cm} / \mathrm{s}$ away from the mirror
Explanation:
C: Given, focal length (f) $=-24 \mathrm{~cm}$
Object distance $(\mathrm{u})=-60 \mathrm{~cm}$
And, initial velocity of object $\left(\mathrm{u}_{\mathrm{i}}\right)=9 \mathrm{~cm} / \mathrm{s}$
Final velocity of object $\left(\mathrm{v}_{\mathrm{f}}\right)=$ ?
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{(-24)}=\frac{1}{(-60)}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{v}}=\frac{1}{60}-\frac{1}{24} \\
\frac{1}{\mathrm{~V}}=\frac{2-5}{120} \\
\mathrm{v}=-\frac{120}{3} \\
\mathrm{v}=-40 \mathrm{~cm}
\end{aligned}$
And, $\quad \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}$
Now, differentiating the above equation with respect to time -
$\begin{aligned}
0=-\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}=-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^2}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}} \quad\left(\because \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{v}_{\mathrm{f}}\right) \\
\mathrm{v}_{\mathrm{f}}=-\left(\frac{-40}{-60}\right)^2 \times \mathrm{u}_{\mathrm{i}} \\
\mathrm{v}_{\mathrm{f}}=-\frac{4}{9} \times 9 \\
\mathrm{v}_{\mathrm{f}}=-4 \mathrm{~cm} / \mathrm{s}
\end{aligned}$
Hence, velocity of image is $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror.
282041
A linear object of height $10 \mathrm{~cm}$ is kept in front of a concave mirror of radius of curature 15 $\mathrm{cm}$, at a distance of $10 \mathrm{~cm}$. The image formed is:
1 magnified and erect
2 magnified and inverted
3 diminished and erect
4 diminished and inverted
Explanation:
B: Given, Object height $\left(\mathrm{h}_{\mathrm{o}}\right)=10 \mathrm{~cm}$
Radius of curvature of mirror $(\mathrm{R})=-15 \mathrm{~cm}$
Focus of mirror $(f)=-\frac{15}{2} \mathrm{~cm}$
Object distance from the mirror $(\mathrm{u})=-10 \mathrm{~cm}$
By using mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{\frac{15}{2}}=-\frac{1}{10}+\frac{1}{\mathrm{~V}} \\
\frac{1}{\mathrm{~V}}=\frac{1}{10}-\frac{2}{15} \\
\frac{1}{\mathrm{~V}}=\frac{3-4}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
We know that,
$\begin{array}{r}
\text { Magnification }(\mathrm{m})=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}} \\
\therefore \quad-\frac{(-30)}{(-10)}=\frac{\mathrm{h}_{\mathrm{i}}}{10} \\
\mathrm{~h}_{\mathrm{i}}=-30 \mathrm{~cm}
\end{array}$
Hence, images are magnified and inverted.
Karnataka CET-2017
Ray Optics
282042
If an object is placed $10 \mathrm{~cm}$ in front of a concave mirror of focal length $20 \mathrm{~cm}$, the image will be
1 diminished, upright, virtual
2 enlarged, upright, virtual
3 diminished, inverted, real
4 enlarged, upright, real
Explanation:
B: Given, object distance $=10 \mathrm{~cm}$
Focal length $=20 \mathrm{~cm}$
From the above value, it is clear that, object is placed between focal length and pole.
Hence, image is enlarge, upright and virtual

CG PET- 2007
Ray Optics
282043
A point object is placed at a distance of $10 \mathrm{~cm}$ and its real image is formed at a distance of $\mathbf{2 0}$ $\mathrm{cm}$ from a concave mirror. If the object is moved by $0.1 \mathrm{~cm}$ towards the mirror, the image will shift by about
1 $0.4 \mathrm{~cm}$ away from the mirror
2 $0.4 \mathrm{~cm}$ towards the mirror
3 $0.8 \mathrm{~cm}$ away from the mirror
4 $0.8 \mathrm{~cm}$ towards the mirror
Explanation:
A: Given, object placed (u) $=-10 \mathrm{~cm}$
Image formed at distance $(\mathrm{v})=-20 \mathrm{~cm}$ (real)
For focal length of concave mirror,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{10}-\frac{1}{20} \\
\frac{1}{\mathrm{f}}=\frac{-1-2}{20}=\frac{-3}{20} \\
\mathrm{f}=-\frac{20}{3}
\end{aligned}$
When object move $0.1 \mathrm{~cm}$ toward the mirror then new position of object -
$\mathrm{u}=10-0.1=9.9 \mathrm{~cm}$
Then, new position of image -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}^{\prime}}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{-\left(\frac{20}{3}\right)}=\frac{1}{-9.9}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-3}{20}+\frac{1}{9.9} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-29.7+20}{20 \times 9.9}
\end{aligned}$
$\begin{aligned}
\mathrm{v}^{\prime} & =\frac{20 \times 9.9}{-9.7} \\
\mathrm{v}^{\prime} & =\frac{-198}{9.7} \\
\mathrm{v}^{\prime} & =-20.4 \mathrm{~cm}
\end{aligned}$
Image shifted $=20.4-20=0.4 \mathrm{~cm}$
Hence, image shifted $0.4 \mathrm{~cm}$ away from the mirror.
CG PET- 2005
Ray Optics
282044
Radius of curvature of concave mirror is $40 \mathrm{~cm}$ and the size of image of real is twice as that of object, then the object distance is
1 $60 \mathrm{~cm}$
2 $20 \mathrm{~cm}$
3 $40 \mathrm{~cm}$
4 $30 \mathrm{~cm}$
Explanation:
D: Given, radius of curvature (R) $=-40 \mathrm{~cm}$
Then, focal length $=-\frac{40}{2}=-20 \mathrm{~cm}$
Magnification $=-2$ (for real image)
$\begin{aligned}
-2=\frac{-\mathrm{v}}{\mathrm{u}} \\
\mathrm{v}=2 \mathrm{u}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{20}=\frac{1}{\mathrm{u}}+\frac{1}{2 \mathrm{u}} \\
-\frac{1}{20}=\frac{3}{2 \mathrm{u}} \\
\mathrm{u}=-30 \mathrm{~cm}
\end{aligned}$
Hence, distance of object is $30 \mathrm{~cm}$.
CG PET- 2007
Ray Optics
282045
A point object is moving on the principal axis of a concave mirror of focal length $24 \mathrm{~cm}$ towards the mirror. When it is at a distance of $60 \mathrm{~cm}$ from the mirror, its velocity is $9 \mathrm{~cm} / \mathrm{s}$. What is the velocity of the image at that instant?
1 $5 \mathrm{~cm} / \mathrm{s}$ towards the mirror
2 $4 \mathrm{~cm} / \mathrm{s}$ towards the mirror
3 $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror
4 $9 \mathrm{~cm} / \mathrm{s}$ away from the mirror
Explanation:
C: Given, focal length (f) $=-24 \mathrm{~cm}$
Object distance $(\mathrm{u})=-60 \mathrm{~cm}$
And, initial velocity of object $\left(\mathrm{u}_{\mathrm{i}}\right)=9 \mathrm{~cm} / \mathrm{s}$
Final velocity of object $\left(\mathrm{v}_{\mathrm{f}}\right)=$ ?
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{(-24)}=\frac{1}{(-60)}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{v}}=\frac{1}{60}-\frac{1}{24} \\
\frac{1}{\mathrm{~V}}=\frac{2-5}{120} \\
\mathrm{v}=-\frac{120}{3} \\
\mathrm{v}=-40 \mathrm{~cm}
\end{aligned}$
And, $\quad \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}$
Now, differentiating the above equation with respect to time -
$\begin{aligned}
0=-\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}=-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^2}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}} \quad\left(\because \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{v}_{\mathrm{f}}\right) \\
\mathrm{v}_{\mathrm{f}}=-\left(\frac{-40}{-60}\right)^2 \times \mathrm{u}_{\mathrm{i}} \\
\mathrm{v}_{\mathrm{f}}=-\frac{4}{9} \times 9 \\
\mathrm{v}_{\mathrm{f}}=-4 \mathrm{~cm} / \mathrm{s}
\end{aligned}$
Hence, velocity of image is $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror.
NEET Test Series from KOTA - 10 Papers In MS WORD
WhatsApp Here
Ray Optics
282041
A linear object of height $10 \mathrm{~cm}$ is kept in front of a concave mirror of radius of curature 15 $\mathrm{cm}$, at a distance of $10 \mathrm{~cm}$. The image formed is:
1 magnified and erect
2 magnified and inverted
3 diminished and erect
4 diminished and inverted
Explanation:
B: Given, Object height $\left(\mathrm{h}_{\mathrm{o}}\right)=10 \mathrm{~cm}$
Radius of curvature of mirror $(\mathrm{R})=-15 \mathrm{~cm}$
Focus of mirror $(f)=-\frac{15}{2} \mathrm{~cm}$
Object distance from the mirror $(\mathrm{u})=-10 \mathrm{~cm}$
By using mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{\frac{15}{2}}=-\frac{1}{10}+\frac{1}{\mathrm{~V}} \\
\frac{1}{\mathrm{~V}}=\frac{1}{10}-\frac{2}{15} \\
\frac{1}{\mathrm{~V}}=\frac{3-4}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
We know that,
$\begin{array}{r}
\text { Magnification }(\mathrm{m})=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}} \\
\therefore \quad-\frac{(-30)}{(-10)}=\frac{\mathrm{h}_{\mathrm{i}}}{10} \\
\mathrm{~h}_{\mathrm{i}}=-30 \mathrm{~cm}
\end{array}$
Hence, images are magnified and inverted.
Karnataka CET-2017
Ray Optics
282042
If an object is placed $10 \mathrm{~cm}$ in front of a concave mirror of focal length $20 \mathrm{~cm}$, the image will be
1 diminished, upright, virtual
2 enlarged, upright, virtual
3 diminished, inverted, real
4 enlarged, upright, real
Explanation:
B: Given, object distance $=10 \mathrm{~cm}$
Focal length $=20 \mathrm{~cm}$
From the above value, it is clear that, object is placed between focal length and pole.
Hence, image is enlarge, upright and virtual

CG PET- 2007
Ray Optics
282043
A point object is placed at a distance of $10 \mathrm{~cm}$ and its real image is formed at a distance of $\mathbf{2 0}$ $\mathrm{cm}$ from a concave mirror. If the object is moved by $0.1 \mathrm{~cm}$ towards the mirror, the image will shift by about
1 $0.4 \mathrm{~cm}$ away from the mirror
2 $0.4 \mathrm{~cm}$ towards the mirror
3 $0.8 \mathrm{~cm}$ away from the mirror
4 $0.8 \mathrm{~cm}$ towards the mirror
Explanation:
A: Given, object placed (u) $=-10 \mathrm{~cm}$
Image formed at distance $(\mathrm{v})=-20 \mathrm{~cm}$ (real)
For focal length of concave mirror,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{10}-\frac{1}{20} \\
\frac{1}{\mathrm{f}}=\frac{-1-2}{20}=\frac{-3}{20} \\
\mathrm{f}=-\frac{20}{3}
\end{aligned}$
When object move $0.1 \mathrm{~cm}$ toward the mirror then new position of object -
$\mathrm{u}=10-0.1=9.9 \mathrm{~cm}$
Then, new position of image -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}^{\prime}}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{-\left(\frac{20}{3}\right)}=\frac{1}{-9.9}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-3}{20}+\frac{1}{9.9} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-29.7+20}{20 \times 9.9}
\end{aligned}$
$\begin{aligned}
\mathrm{v}^{\prime} & =\frac{20 \times 9.9}{-9.7} \\
\mathrm{v}^{\prime} & =\frac{-198}{9.7} \\
\mathrm{v}^{\prime} & =-20.4 \mathrm{~cm}
\end{aligned}$
Image shifted $=20.4-20=0.4 \mathrm{~cm}$
Hence, image shifted $0.4 \mathrm{~cm}$ away from the mirror.
CG PET- 2005
Ray Optics
282044
Radius of curvature of concave mirror is $40 \mathrm{~cm}$ and the size of image of real is twice as that of object, then the object distance is
1 $60 \mathrm{~cm}$
2 $20 \mathrm{~cm}$
3 $40 \mathrm{~cm}$
4 $30 \mathrm{~cm}$
Explanation:
D: Given, radius of curvature (R) $=-40 \mathrm{~cm}$
Then, focal length $=-\frac{40}{2}=-20 \mathrm{~cm}$
Magnification $=-2$ (for real image)
$\begin{aligned}
-2=\frac{-\mathrm{v}}{\mathrm{u}} \\
\mathrm{v}=2 \mathrm{u}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{20}=\frac{1}{\mathrm{u}}+\frac{1}{2 \mathrm{u}} \\
-\frac{1}{20}=\frac{3}{2 \mathrm{u}} \\
\mathrm{u}=-30 \mathrm{~cm}
\end{aligned}$
Hence, distance of object is $30 \mathrm{~cm}$.
CG PET- 2007
Ray Optics
282045
A point object is moving on the principal axis of a concave mirror of focal length $24 \mathrm{~cm}$ towards the mirror. When it is at a distance of $60 \mathrm{~cm}$ from the mirror, its velocity is $9 \mathrm{~cm} / \mathrm{s}$. What is the velocity of the image at that instant?
1 $5 \mathrm{~cm} / \mathrm{s}$ towards the mirror
2 $4 \mathrm{~cm} / \mathrm{s}$ towards the mirror
3 $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror
4 $9 \mathrm{~cm} / \mathrm{s}$ away from the mirror
Explanation:
C: Given, focal length (f) $=-24 \mathrm{~cm}$
Object distance $(\mathrm{u})=-60 \mathrm{~cm}$
And, initial velocity of object $\left(\mathrm{u}_{\mathrm{i}}\right)=9 \mathrm{~cm} / \mathrm{s}$
Final velocity of object $\left(\mathrm{v}_{\mathrm{f}}\right)=$ ?
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{(-24)}=\frac{1}{(-60)}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{v}}=\frac{1}{60}-\frac{1}{24} \\
\frac{1}{\mathrm{~V}}=\frac{2-5}{120} \\
\mathrm{v}=-\frac{120}{3} \\
\mathrm{v}=-40 \mathrm{~cm}
\end{aligned}$
And, $\quad \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}$
Now, differentiating the above equation with respect to time -
$\begin{aligned}
0=-\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}=-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^2}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}} \quad\left(\because \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{v}_{\mathrm{f}}\right) \\
\mathrm{v}_{\mathrm{f}}=-\left(\frac{-40}{-60}\right)^2 \times \mathrm{u}_{\mathrm{i}} \\
\mathrm{v}_{\mathrm{f}}=-\frac{4}{9} \times 9 \\
\mathrm{v}_{\mathrm{f}}=-4 \mathrm{~cm} / \mathrm{s}
\end{aligned}$
Hence, velocity of image is $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror.
282041
A linear object of height $10 \mathrm{~cm}$ is kept in front of a concave mirror of radius of curature 15 $\mathrm{cm}$, at a distance of $10 \mathrm{~cm}$. The image formed is:
1 magnified and erect
2 magnified and inverted
3 diminished and erect
4 diminished and inverted
Explanation:
B: Given, Object height $\left(\mathrm{h}_{\mathrm{o}}\right)=10 \mathrm{~cm}$
Radius of curvature of mirror $(\mathrm{R})=-15 \mathrm{~cm}$
Focus of mirror $(f)=-\frac{15}{2} \mathrm{~cm}$
Object distance from the mirror $(\mathrm{u})=-10 \mathrm{~cm}$
By using mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{\frac{15}{2}}=-\frac{1}{10}+\frac{1}{\mathrm{~V}} \\
\frac{1}{\mathrm{~V}}=\frac{1}{10}-\frac{2}{15} \\
\frac{1}{\mathrm{~V}}=\frac{3-4}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
We know that,
$\begin{array}{r}
\text { Magnification }(\mathrm{m})=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}} \\
\therefore \quad-\frac{(-30)}{(-10)}=\frac{\mathrm{h}_{\mathrm{i}}}{10} \\
\mathrm{~h}_{\mathrm{i}}=-30 \mathrm{~cm}
\end{array}$
Hence, images are magnified and inverted.
Karnataka CET-2017
Ray Optics
282042
If an object is placed $10 \mathrm{~cm}$ in front of a concave mirror of focal length $20 \mathrm{~cm}$, the image will be
1 diminished, upright, virtual
2 enlarged, upright, virtual
3 diminished, inverted, real
4 enlarged, upright, real
Explanation:
B: Given, object distance $=10 \mathrm{~cm}$
Focal length $=20 \mathrm{~cm}$
From the above value, it is clear that, object is placed between focal length and pole.
Hence, image is enlarge, upright and virtual

CG PET- 2007
Ray Optics
282043
A point object is placed at a distance of $10 \mathrm{~cm}$ and its real image is formed at a distance of $\mathbf{2 0}$ $\mathrm{cm}$ from a concave mirror. If the object is moved by $0.1 \mathrm{~cm}$ towards the mirror, the image will shift by about
1 $0.4 \mathrm{~cm}$ away from the mirror
2 $0.4 \mathrm{~cm}$ towards the mirror
3 $0.8 \mathrm{~cm}$ away from the mirror
4 $0.8 \mathrm{~cm}$ towards the mirror
Explanation:
A: Given, object placed (u) $=-10 \mathrm{~cm}$
Image formed at distance $(\mathrm{v})=-20 \mathrm{~cm}$ (real)
For focal length of concave mirror,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{10}-\frac{1}{20} \\
\frac{1}{\mathrm{f}}=\frac{-1-2}{20}=\frac{-3}{20} \\
\mathrm{f}=-\frac{20}{3}
\end{aligned}$
When object move $0.1 \mathrm{~cm}$ toward the mirror then new position of object -
$\mathrm{u}=10-0.1=9.9 \mathrm{~cm}$
Then, new position of image -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}^{\prime}}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{-\left(\frac{20}{3}\right)}=\frac{1}{-9.9}+\frac{1}{\mathrm{~V}^{\prime}} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-3}{20}+\frac{1}{9.9} \\
\frac{1}{\mathrm{~V}^{\prime}}=\frac{-29.7+20}{20 \times 9.9}
\end{aligned}$
$\begin{aligned}
\mathrm{v}^{\prime} & =\frac{20 \times 9.9}{-9.7} \\
\mathrm{v}^{\prime} & =\frac{-198}{9.7} \\
\mathrm{v}^{\prime} & =-20.4 \mathrm{~cm}
\end{aligned}$
Image shifted $=20.4-20=0.4 \mathrm{~cm}$
Hence, image shifted $0.4 \mathrm{~cm}$ away from the mirror.
CG PET- 2005
Ray Optics
282044
Radius of curvature of concave mirror is $40 \mathrm{~cm}$ and the size of image of real is twice as that of object, then the object distance is
1 $60 \mathrm{~cm}$
2 $20 \mathrm{~cm}$
3 $40 \mathrm{~cm}$
4 $30 \mathrm{~cm}$
Explanation:
D: Given, radius of curvature (R) $=-40 \mathrm{~cm}$
Then, focal length $=-\frac{40}{2}=-20 \mathrm{~cm}$
Magnification $=-2$ (for real image)
$\begin{aligned}
-2=\frac{-\mathrm{v}}{\mathrm{u}} \\
\mathrm{v}=2 \mathrm{u}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
-\frac{1}{20}=\frac{1}{\mathrm{u}}+\frac{1}{2 \mathrm{u}} \\
-\frac{1}{20}=\frac{3}{2 \mathrm{u}} \\
\mathrm{u}=-30 \mathrm{~cm}
\end{aligned}$
Hence, distance of object is $30 \mathrm{~cm}$.
CG PET- 2007
Ray Optics
282045
A point object is moving on the principal axis of a concave mirror of focal length $24 \mathrm{~cm}$ towards the mirror. When it is at a distance of $60 \mathrm{~cm}$ from the mirror, its velocity is $9 \mathrm{~cm} / \mathrm{s}$. What is the velocity of the image at that instant?
1 $5 \mathrm{~cm} / \mathrm{s}$ towards the mirror
2 $4 \mathrm{~cm} / \mathrm{s}$ towards the mirror
3 $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror
4 $9 \mathrm{~cm} / \mathrm{s}$ away from the mirror
Explanation:
C: Given, focal length (f) $=-24 \mathrm{~cm}$
Object distance $(\mathrm{u})=-60 \mathrm{~cm}$
And, initial velocity of object $\left(\mathrm{u}_{\mathrm{i}}\right)=9 \mathrm{~cm} / \mathrm{s}$
Final velocity of object $\left(\mathrm{v}_{\mathrm{f}}\right)=$ ?
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{(-24)}=\frac{1}{(-60)}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{v}}=\frac{1}{60}-\frac{1}{24} \\
\frac{1}{\mathrm{~V}}=\frac{2-5}{120} \\
\mathrm{v}=-\frac{120}{3} \\
\mathrm{v}=-40 \mathrm{~cm}
\end{aligned}$
And, $\quad \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}$
Now, differentiating the above equation with respect to time -
$\begin{aligned}
0=-\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{1}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}}=-\frac{1}{\mathrm{v}^2} \frac{\mathrm{dv}}{\mathrm{dt}} \\
\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^2}{\mathrm{u}^2} \frac{\mathrm{du}}{\mathrm{dt}} \quad\left(\because \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{v}_{\mathrm{f}}\right) \\
\mathrm{v}_{\mathrm{f}}=-\left(\frac{-40}{-60}\right)^2 \times \mathrm{u}_{\mathrm{i}} \\
\mathrm{v}_{\mathrm{f}}=-\frac{4}{9} \times 9 \\
\mathrm{v}_{\mathrm{f}}=-4 \mathrm{~cm} / \mathrm{s}
\end{aligned}$
Hence, velocity of image is $4 \mathrm{~cm} / \mathrm{s}$ away from the mirror.