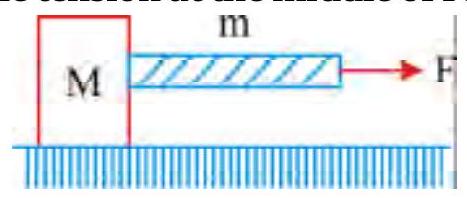
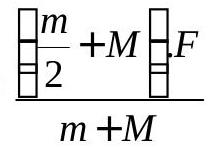270243 A ball is suspended by a thread from the ceiling of atram car. The brakes are applied and the speed of the car changes uniformly from 36 \(\mathbf{k m h}^{-1}\) to zero in \(5 \mathrm{~s}\). The angle by which the ball deviates from the vertical is \(\left(\mathrm{g}=\mathbf{1 0} \mathbf{~ m s}^{-2}\right)\)
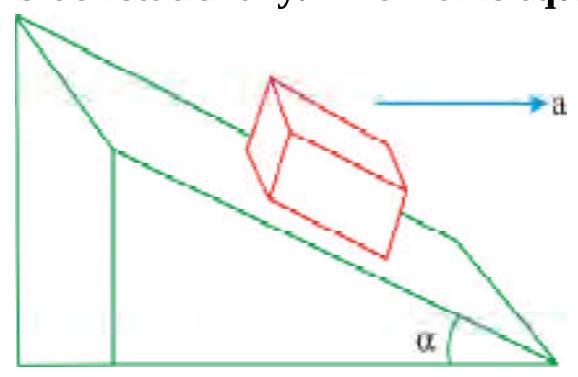
270245 A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs\(1,000 \mathrm{~N}\) exerts a force of 450 \(\mathrm{N}\) on the chair downwards while pulling the rope on the other side. If the chair weighs \(250 \mathrm{~N}\), then the acceleration of the chair is
270243 A ball is suspended by a thread from the ceiling of atram car. The brakes are applied and the speed of the car changes uniformly from 36 \(\mathbf{k m h}^{-1}\) to zero in \(5 \mathrm{~s}\). The angle by which the ball deviates from the vertical is \(\left(\mathrm{g}=\mathbf{1 0} \mathbf{~ m s}^{-2}\right)\)
270245 A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs\(1,000 \mathrm{~N}\) exerts a force of 450 \(\mathrm{N}\) on the chair downwards while pulling the rope on the other side. If the chair weighs \(250 \mathrm{~N}\), then the acceleration of the chair is
270243 A ball is suspended by a thread from the ceiling of atram car. The brakes are applied and the speed of the car changes uniformly from 36 \(\mathbf{k m h}^{-1}\) to zero in \(5 \mathrm{~s}\). The angle by which the ball deviates from the vertical is \(\left(\mathrm{g}=\mathbf{1 0} \mathbf{~ m s}^{-2}\right)\)
270245 A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs\(1,000 \mathrm{~N}\) exerts a force of 450 \(\mathrm{N}\) on the chair downwards while pulling the rope on the other side. If the chair weighs \(250 \mathrm{~N}\), then the acceleration of the chair is
270243 A ball is suspended by a thread from the ceiling of atram car. The brakes are applied and the speed of the car changes uniformly from 36 \(\mathbf{k m h}^{-1}\) to zero in \(5 \mathrm{~s}\). The angle by which the ball deviates from the vertical is \(\left(\mathrm{g}=\mathbf{1 0} \mathbf{~ m s}^{-2}\right)\)
270245 A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs\(1,000 \mathrm{~N}\) exerts a force of 450 \(\mathrm{N}\) on the chair downwards while pulling the rope on the other side. If the chair weighs \(250 \mathrm{~N}\), then the acceleration of the chair is