270250 Consider three blocks of masses \(m_{1}, m_{2}, m_{3}\) interconnected by strings which are pulled by a common force \(F\) on a frictionless horizontal table as in the figure. The tension\(T_{1}\) and \(T_{2}\) are also indicated

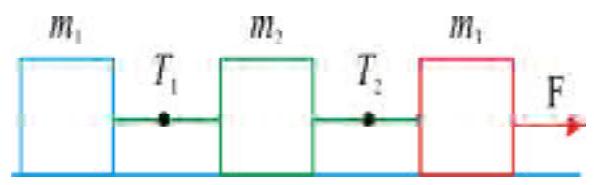
a) \(T_{2}\lt T_{1}\) if \(m_{2}\lt m_{1}\)
b) \(T_{2}=T_{1}\) if \(m_{2}=m_{1}\)
c) \(T_{2}\lt T_{1}\) always
d) acceleration of the system \(=\frac{F}{m_{1}+m_{2}+m_{3}}\)

270251 A railway engine of mass 50 tons is pulling a wagon of mass 40 tons with a force of\(4500 \mathrm{~N}\). The resistance force acting is \(1 \mathrm{~N}\) per ton. The tension in the coupling between the engine and the wagon is

270252 In the following figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain distance with force '\(P\) ' will be

270253 Two identical blocks each of mass" \(M\) " are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that it has an acceleration of \(1 / 5^{\text {th }}\) of the acceleration due to gravity

270250 Consider three blocks of masses \(m_{1}, m_{2}, m_{3}\) interconnected by strings which are pulled by a common force \(F\) on a frictionless horizontal table as in the figure. The tension\(T_{1}\) and \(T_{2}\) are also indicated

a) \(T_{2}\lt T_{1}\) if \(m_{2}\lt m_{1}\)
b) \(T_{2}=T_{1}\) if \(m_{2}=m_{1}\)
c) \(T_{2}\lt T_{1}\) always
d) acceleration of the system \(=\frac{F}{m_{1}+m_{2}+m_{3}}\)

270251 A railway engine of mass 50 tons is pulling a wagon of mass 40 tons with a force of\(4500 \mathrm{~N}\). The resistance force acting is \(1 \mathrm{~N}\) per ton. The tension in the coupling between the engine and the wagon is

270252 In the following figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain distance with force '\(P\) ' will be

270253 Two identical blocks each of mass" \(M\) " are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that it has an acceleration of \(1 / 5^{\text {th }}\) of the acceleration due to gravity

270250 Consider three blocks of masses \(m_{1}, m_{2}, m_{3}\) interconnected by strings which are pulled by a common force \(F\) on a frictionless horizontal table as in the figure. The tension\(T_{1}\) and \(T_{2}\) are also indicated

a) \(T_{2}\lt T_{1}\) if \(m_{2}\lt m_{1}\)
b) \(T_{2}=T_{1}\) if \(m_{2}=m_{1}\)
c) \(T_{2}\lt T_{1}\) always
d) acceleration of the system \(=\frac{F}{m_{1}+m_{2}+m_{3}}\)

270251 A railway engine of mass 50 tons is pulling a wagon of mass 40 tons with a force of\(4500 \mathrm{~N}\). The resistance force acting is \(1 \mathrm{~N}\) per ton. The tension in the coupling between the engine and the wagon is

270252 In the following figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain distance with force '\(P\) ' will be

270253 Two identical blocks each of mass" \(M\) " are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that it has an acceleration of \(1 / 5^{\text {th }}\) of the acceleration due to gravity

270250 Consider three blocks of masses \(m_{1}, m_{2}, m_{3}\) interconnected by strings which are pulled by a common force \(F\) on a frictionless horizontal table as in the figure. The tension\(T_{1}\) and \(T_{2}\) are also indicated

a) \(T_{2}\lt T_{1}\) if \(m_{2}\lt m_{1}\)
b) \(T_{2}=T_{1}\) if \(m_{2}=m_{1}\)
c) \(T_{2}\lt T_{1}\) always
d) acceleration of the system \(=\frac{F}{m_{1}+m_{2}+m_{3}}\)

270251 A railway engine of mass 50 tons is pulling a wagon of mass 40 tons with a force of\(4500 \mathrm{~N}\). The resistance force acting is \(1 \mathrm{~N}\) per ton. The tension in the coupling between the engine and the wagon is

270252 In the following figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain distance with force '\(P\) ' will be

270253 Two identical blocks each of mass" \(M\) " are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that it has an acceleration of \(1 / 5^{\text {th }}\) of the acceleration due to gravity