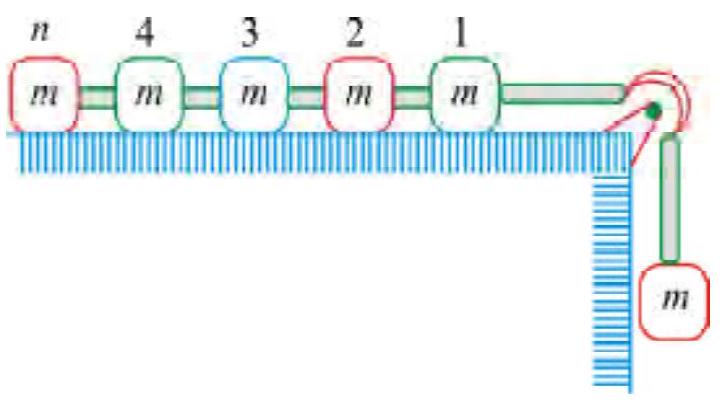
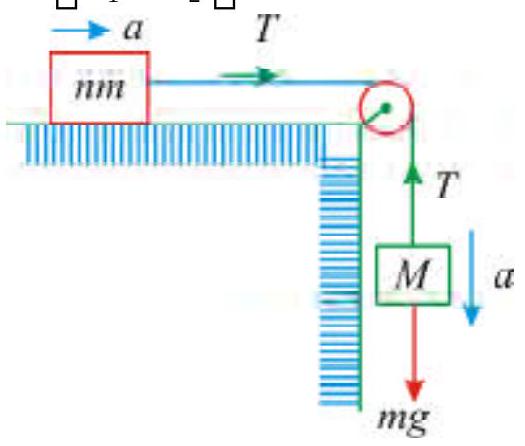
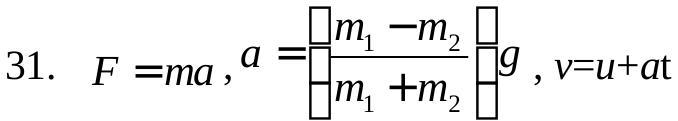270256
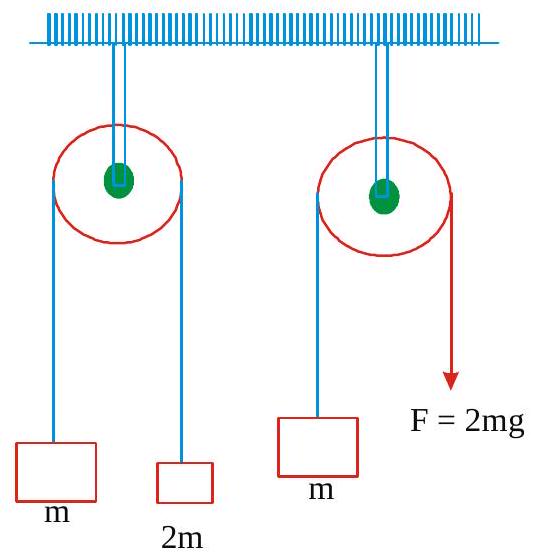
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case\(I\),the mass \(m\) is lifted by attaching a mass \(2 \mathrm{~m}\) to the other end of rope with a constant downward force \(F=2 \mathrm{mg}\), where \(g\) is acceleration due to gravity. The acceleration of mass \(m\) in case \(I\) is
270257
Two masses of\(10 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are suspended from a rigid support as shown in figure. The system is pulled down with a force of \(150 \mathrm{~N}\) attached to the lower mass. The string attached to the support breaks and the system accelerates downwards.
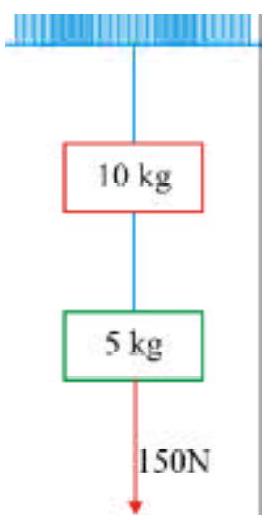
In case the force continues to act.what will be the tension acting between the two masses?
270258 Two bodies of masses\(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the \(3 \mathrm{~kg}\) body after one second is \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270256
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case\(I\),the mass \(m\) is lifted by attaching a mass \(2 \mathrm{~m}\) to the other end of rope with a constant downward force \(F=2 \mathrm{mg}\), where \(g\) is acceleration due to gravity. The acceleration of mass \(m\) in case \(I\) is

270257
Two masses of\(10 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are suspended from a rigid support as shown in figure. The system is pulled down with a force of \(150 \mathrm{~N}\) attached to the lower mass. The string attached to the support breaks and the system accelerates downwards.

In case the force continues to act.what will be the tension acting between the two masses?
270258 Two bodies of masses\(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the \(3 \mathrm{~kg}\) body after one second is \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270256
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case\(I\),the mass \(m\) is lifted by attaching a mass \(2 \mathrm{~m}\) to the other end of rope with a constant downward force \(F=2 \mathrm{mg}\), where \(g\) is acceleration due to gravity. The acceleration of mass \(m\) in case \(I\) is

270257
Two masses of\(10 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are suspended from a rigid support as shown in figure. The system is pulled down with a force of \(150 \mathrm{~N}\) attached to the lower mass. The string attached to the support breaks and the system accelerates downwards.

In case the force continues to act.what will be the tension acting between the two masses?
270258 Two bodies of masses\(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the \(3 \mathrm{~kg}\) body after one second is \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270256
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case\(I\),the mass \(m\) is lifted by attaching a mass \(2 \mathrm{~m}\) to the other end of rope with a constant downward force \(F=2 \mathrm{mg}\), where \(g\) is acceleration due to gravity. The acceleration of mass \(m\) in case \(I\) is

270257
Two masses of\(10 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are suspended from a rigid support as shown in figure. The system is pulled down with a force of \(150 \mathrm{~N}\) attached to the lower mass. The string attached to the support breaks and the system accelerates downwards.

In case the force continues to act.what will be the tension acting between the two masses?
270258 Two bodies of masses\(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the \(3 \mathrm{~kg}\) body after one second is \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270256
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case\(I\),the mass \(m\) is lifted by attaching a mass \(2 \mathrm{~m}\) to the other end of rope with a constant downward force \(F=2 \mathrm{mg}\), where \(g\) is acceleration due to gravity. The acceleration of mass \(m\) in case \(I\) is

270257
Two masses of\(10 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are suspended from a rigid support as shown in figure. The system is pulled down with a force of \(150 \mathrm{~N}\) attached to the lower mass. The string attached to the support breaks and the system accelerates downwards.

In case the force continues to act.what will be the tension acting between the two masses?
270258 Two bodies of masses\(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the \(3 \mathrm{~kg}\) body after one second is \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)