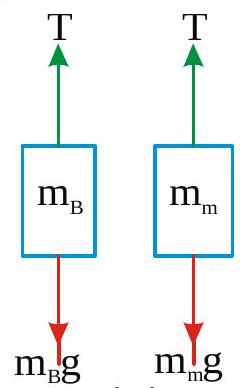
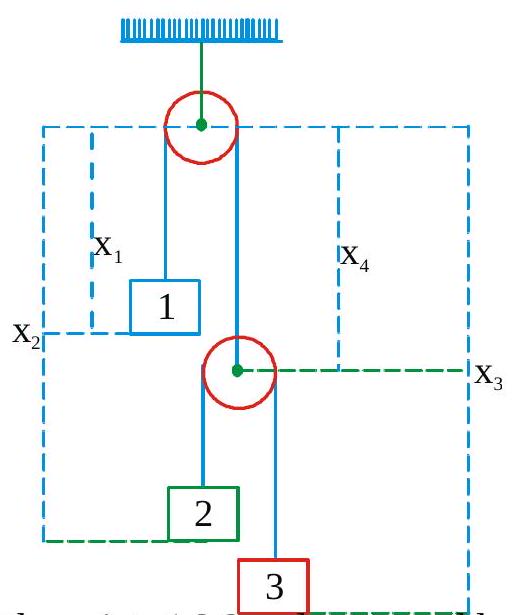
270351 A ropeis stretched between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has a mass of \(250 \mathrm{~kg}\) where as the mass of second boat is double of this mass. If the initial distance between the boats was \(100 \mathrm{~m}\), the time taken for two boats to meet each other in seconds (neglect water resistance between boats and water)

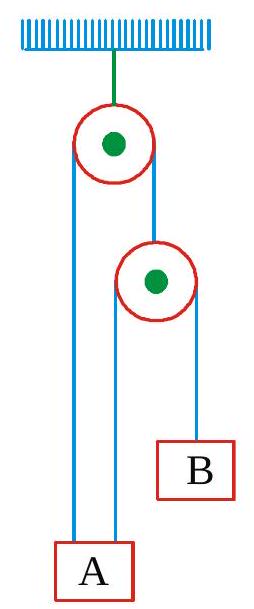
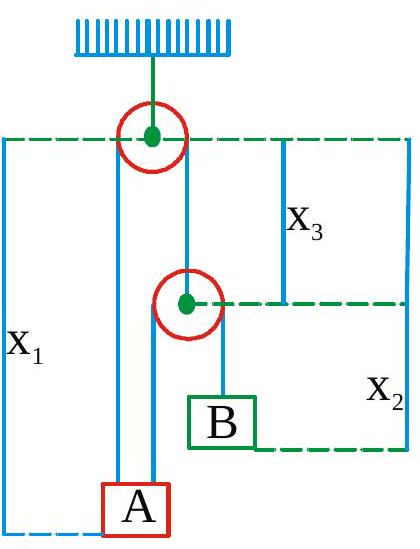
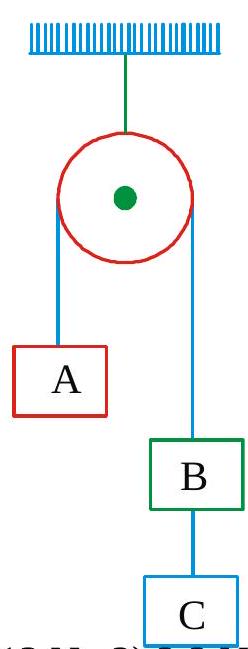
270352 In order to raise a block of mass\(100 \mathrm{~kg}\) a man of mass \(60 \mathrm{~kg}\) fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with an acceleration \(\frac{5 g}{4}\) relative to rope. The tension in the rope is \(\left(g=10 \mathrm{~ms}^{-2}\right)\)

270353 In the pulley-block arrangement shown infigure.Find the relation between acceleration of block \(A\) and \(B\).

270354 Three equal weights\(A, B\) and \(C\) of mass \(2 \mathrm{~kg}\) each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights \(B\) and \(C\) is

270355 In the figure show\(n a_{3}=6 \mathrm{~m} / \mathrm{s}^{2}\) (downwards) and \(a_{2}=4 m / s^{2}\) (upwards). Find acceleration of 

270351 A ropeis stretched between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has a mass of \(250 \mathrm{~kg}\) where as the mass of second boat is double of this mass. If the initial distance between the boats was \(100 \mathrm{~m}\), the time taken for two boats to meet each other in seconds (neglect water resistance between boats and water)

270352 In order to raise a block of mass\(100 \mathrm{~kg}\) a man of mass \(60 \mathrm{~kg}\) fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with an acceleration \(\frac{5 g}{4}\) relative to rope. The tension in the rope is \(\left(g=10 \mathrm{~ms}^{-2}\right)\)

270353 In the pulley-block arrangement shown infigure.Find the relation between acceleration of block \(A\) and \(B\).

270354 Three equal weights\(A, B\) and \(C\) of mass \(2 \mathrm{~kg}\) each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights \(B\) and \(C\) is

270355 In the figure show\(n a_{3}=6 \mathrm{~m} / \mathrm{s}^{2}\) (downwards) and \(a_{2}=4 m / s^{2}\) (upwards). Find acceleration of 

270351 A ropeis stretched between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has a mass of \(250 \mathrm{~kg}\) where as the mass of second boat is double of this mass. If the initial distance between the boats was \(100 \mathrm{~m}\), the time taken for two boats to meet each other in seconds (neglect water resistance between boats and water)

270352 In order to raise a block of mass\(100 \mathrm{~kg}\) a man of mass \(60 \mathrm{~kg}\) fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with an acceleration \(\frac{5 g}{4}\) relative to rope. The tension in the rope is \(\left(g=10 \mathrm{~ms}^{-2}\right)\)

270353 In the pulley-block arrangement shown infigure.Find the relation between acceleration of block \(A\) and \(B\).

270354 Three equal weights\(A, B\) and \(C\) of mass \(2 \mathrm{~kg}\) each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights \(B\) and \(C\) is

270355 In the figure show\(n a_{3}=6 \mathrm{~m} / \mathrm{s}^{2}\) (downwards) and \(a_{2}=4 m / s^{2}\) (upwards). Find acceleration of 

270351 A ropeis stretched between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has a mass of \(250 \mathrm{~kg}\) where as the mass of second boat is double of this mass. If the initial distance between the boats was \(100 \mathrm{~m}\), the time taken for two boats to meet each other in seconds (neglect water resistance between boats and water)

270352 In order to raise a block of mass\(100 \mathrm{~kg}\) a man of mass \(60 \mathrm{~kg}\) fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with an acceleration \(\frac{5 g}{4}\) relative to rope. The tension in the rope is \(\left(g=10 \mathrm{~ms}^{-2}\right)\)

270353 In the pulley-block arrangement shown infigure.Find the relation between acceleration of block \(A\) and \(B\).

270354 Three equal weights\(A, B\) and \(C\) of mass \(2 \mathrm{~kg}\) each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights \(B\) and \(C\) is

270355 In the figure show\(n a_{3}=6 \mathrm{~m} / \mathrm{s}^{2}\) (downwards) and \(a_{2}=4 m / s^{2}\) (upwards). Find acceleration of 

270351 A ropeis stretched between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has a mass of \(250 \mathrm{~kg}\) where as the mass of second boat is double of this mass. If the initial distance between the boats was \(100 \mathrm{~m}\), the time taken for two boats to meet each other in seconds (neglect water resistance between boats and water)

270352 In order to raise a block of mass\(100 \mathrm{~kg}\) a man of mass \(60 \mathrm{~kg}\) fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with an acceleration \(\frac{5 g}{4}\) relative to rope. The tension in the rope is \(\left(g=10 \mathrm{~ms}^{-2}\right)\)

270353 In the pulley-block arrangement shown infigure.Find the relation between acceleration of block \(A\) and \(B\).

270354 Three equal weights\(A, B\) and \(C\) of mass \(2 \mathrm{~kg}\) each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights \(B\) and \(C\) is

270355 In the figure show\(n a_{3}=6 \mathrm{~m} / \mathrm{s}^{2}\) (downwards) and \(a_{2}=4 m / s^{2}\) (upwards). Find acceleration of