270356
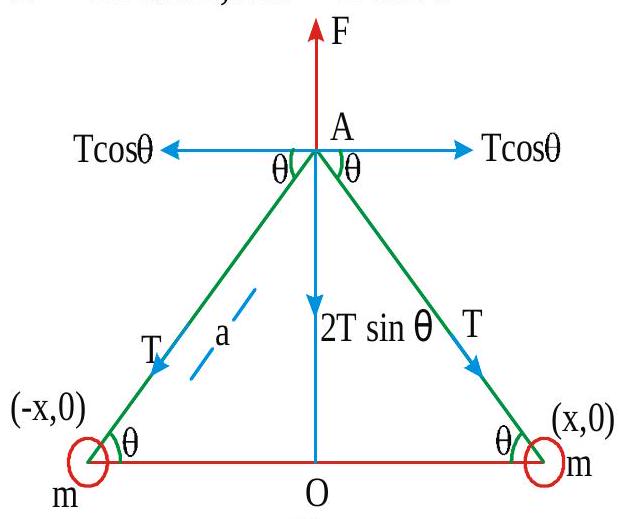
A man of mass\(m\) stands on a platform of equal mass \(m\) and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be

270358
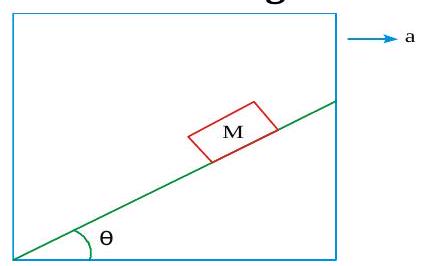
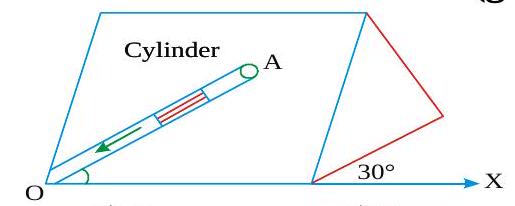
An inclined plane makes an angle\(30^{\circ}\) with the horizontal. A groove (OA) of length \(5 \mathrm{~m}\) cut, in the plane makes an angle \(30^{\circ}\) with \(O X\). A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to \(O\) is \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270359
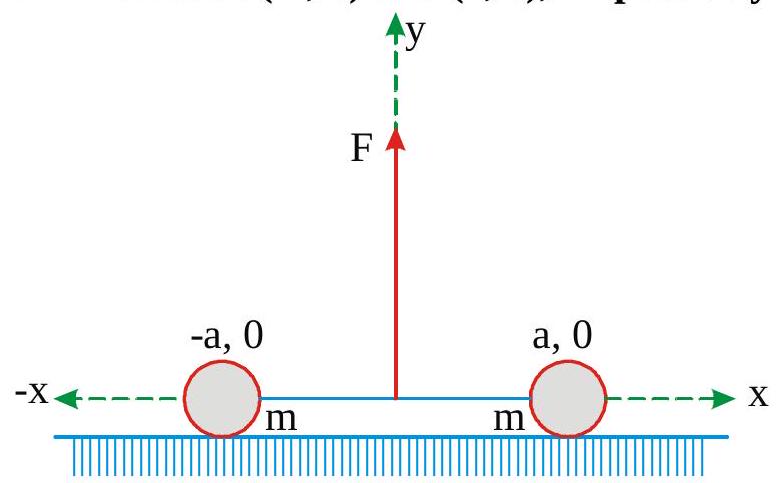
Two masses each equal to\(m\) are lying on \(X\) axis at \((-a, 0)\) and \((+a, 0)\), respectively, as shown in fig. They are connected by a light string. A force \(F\) is applied at the origin along vertical direction. As a result, the masses move towards each other without loosing contact with ground. What is the acceleration of each mass? Assume the instantaneous position of the masses as \((-\mathrm{x}, 0)\) and \((\mathrm{x}, 0)\), respectively
270356
A man of mass\(m\) stands on a platform of equal mass \(m\) and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be

270358
An inclined plane makes an angle\(30^{\circ}\) with the horizontal. A groove (OA) of length \(5 \mathrm{~m}\) cut, in the plane makes an angle \(30^{\circ}\) with \(O X\). A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to \(O\) is \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

270359
Two masses each equal to\(m\) are lying on \(X\) axis at \((-a, 0)\) and \((+a, 0)\), respectively, as shown in fig. They are connected by a light string. A force \(F\) is applied at the origin along vertical direction. As a result, the masses move towards each other without loosing contact with ground. What is the acceleration of each mass? Assume the instantaneous position of the masses as \((-\mathrm{x}, 0)\) and \((\mathrm{x}, 0)\), respectively

270356
A man of mass\(m\) stands on a platform of equal mass \(m\) and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be

270358
An inclined plane makes an angle\(30^{\circ}\) with the horizontal. A groove (OA) of length \(5 \mathrm{~m}\) cut, in the plane makes an angle \(30^{\circ}\) with \(O X\). A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to \(O\) is \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

270359
Two masses each equal to\(m\) are lying on \(X\) axis at \((-a, 0)\) and \((+a, 0)\), respectively, as shown in fig. They are connected by a light string. A force \(F\) is applied at the origin along vertical direction. As a result, the masses move towards each other without loosing contact with ground. What is the acceleration of each mass? Assume the instantaneous position of the masses as \((-\mathrm{x}, 0)\) and \((\mathrm{x}, 0)\), respectively

270356
A man of mass\(m\) stands on a platform of equal mass \(m\) and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be

270358
An inclined plane makes an angle\(30^{\circ}\) with the horizontal. A groove (OA) of length \(5 \mathrm{~m}\) cut, in the plane makes an angle \(30^{\circ}\) with \(O X\). A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to \(O\) is \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

270359
Two masses each equal to\(m\) are lying on \(X\) axis at \((-a, 0)\) and \((+a, 0)\), respectively, as shown in fig. They are connected by a light string. A force \(F\) is applied at the origin along vertical direction. As a result, the masses move towards each other without loosing contact with ground. What is the acceleration of each mass? Assume the instantaneous position of the masses as \((-\mathrm{x}, 0)\) and \((\mathrm{x}, 0)\), respectively