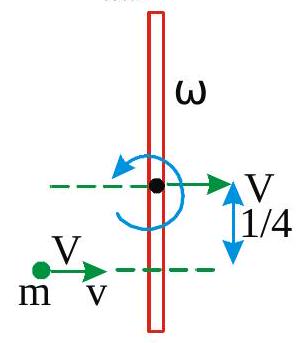
269633 A uniform smooth rod (mass \(m\) and length \(l\) ) placed on a smooth horizontal floor is hit by a particle (mass \(\mathrm{m}\) ) moving on the floor, at a distance \(l / 4\) from one end elastically \((\mathrm{e}=1)\).The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
269633 A uniform smooth rod (mass \(m\) and length \(l\) ) placed on a smooth horizontal floor is hit by a particle (mass \(\mathrm{m}\) ) moving on the floor, at a distance \(l / 4\) from one end elastically \((\mathrm{e}=1)\).The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
269633 A uniform smooth rod (mass \(m\) and length \(l\) ) placed on a smooth horizontal floor is hit by a particle (mass \(\mathrm{m}\) ) moving on the floor, at a distance \(l / 4\) from one end elastically \((\mathrm{e}=1)\).The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
269633 A uniform smooth rod (mass \(m\) and length \(l\) ) placed on a smooth horizontal floor is hit by a particle (mass \(\mathrm{m}\) ) moving on the floor, at a distance \(l / 4\) from one end elastically \((\mathrm{e}=1)\).The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be