269637
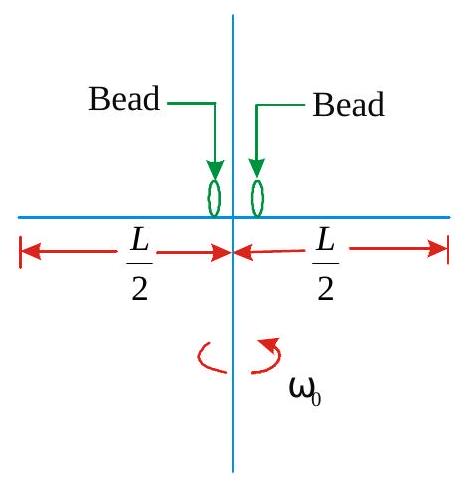
A smooth uniform rod of length \(L\) and mass \(M\) has two identical beads of negligible size, each of mass \(m\), which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with angular velocity \(\omega_{0}\) about its axis perpendicular to the rodand passing through its mid point (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is
\([\) [
269640
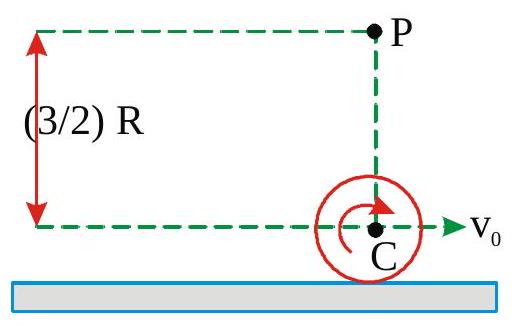
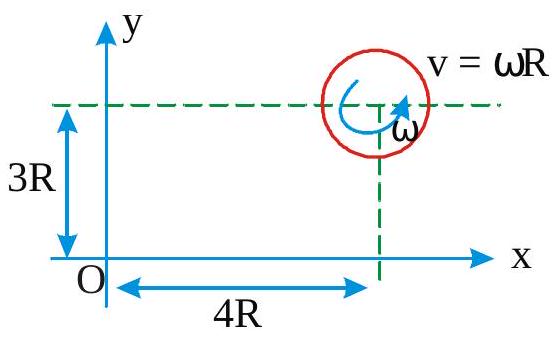
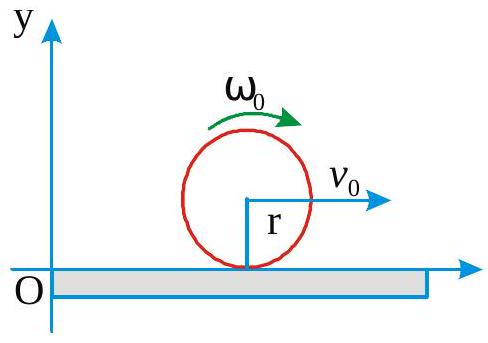
A uniform sphere of mass \(m\), radius \(r\) and moment of inertia I about its centre of mass axis moves along the \(x\)-axis is shown in figure. Its centre of mass moves with velocity \(\mathbf{v}_{0}\),and it rotates about its centre of mass with angular velocity \(\omega_{0}\). Let \(L=\left(I \omega_{0}+m v_{0} r\right)(-k)\). The angular momentum of the body about the the origin \(O\) is
269637
A smooth uniform rod of length \(L\) and mass \(M\) has two identical beads of negligible size, each of mass \(m\), which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with angular velocity \(\omega_{0}\) about its axis perpendicular to the rodand passing through its mid point (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is
\([\) [

269640
A uniform sphere of mass \(m\), radius \(r\) and moment of inertia I about its centre of mass axis moves along the \(x\)-axis is shown in figure. Its centre of mass moves with velocity \(\mathbf{v}_{0}\),and it rotates about its centre of mass with angular velocity \(\omega_{0}\). Let \(L=\left(I \omega_{0}+m v_{0} r\right)(-k)\). The angular momentum of the body about the the origin \(O\) is

269637
A smooth uniform rod of length \(L\) and mass \(M\) has two identical beads of negligible size, each of mass \(m\), which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with angular velocity \(\omega_{0}\) about its axis perpendicular to the rodand passing through its mid point (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is
\([\) [

269640
A uniform sphere of mass \(m\), radius \(r\) and moment of inertia I about its centre of mass axis moves along the \(x\)-axis is shown in figure. Its centre of mass moves with velocity \(\mathbf{v}_{0}\),and it rotates about its centre of mass with angular velocity \(\omega_{0}\). Let \(L=\left(I \omega_{0}+m v_{0} r\right)(-k)\). The angular momentum of the body about the the origin \(O\) is

269637
A smooth uniform rod of length \(L\) and mass \(M\) has two identical beads of negligible size, each of mass \(m\), which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with angular velocity \(\omega_{0}\) about its axis perpendicular to the rodand passing through its mid point (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is
\([\) [

269640
A uniform sphere of mass \(m\), radius \(r\) and moment of inertia I about its centre of mass axis moves along the \(x\)-axis is shown in figure. Its centre of mass moves with velocity \(\mathbf{v}_{0}\),and it rotates about its centre of mass with angular velocity \(\omega_{0}\). Let \(L=\left(I \omega_{0}+m v_{0} r\right)(-k)\). The angular momentum of the body about the the origin \(O\) is