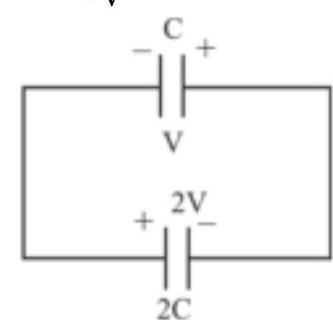
165711 A parallel plate capacitor of capacitance $C$ is connected to a battery and is charged to a potential difference $V$. Another capacitor of capacitance $2 \mathrm{C}$ is similarly charge to a potential difference $2 \mathrm{~V}$. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
165711 A parallel plate capacitor of capacitance $C$ is connected to a battery and is charged to a potential difference $V$. Another capacitor of capacitance $2 \mathrm{C}$ is similarly charge to a potential difference $2 \mathrm{~V}$. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
165711 A parallel plate capacitor of capacitance $C$ is connected to a battery and is charged to a potential difference $V$. Another capacitor of capacitance $2 \mathrm{C}$ is similarly charge to a potential difference $2 \mathrm{~V}$. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
165711 A parallel plate capacitor of capacitance $C$ is connected to a battery and is charged to a potential difference $V$. Another capacitor of capacitance $2 \mathrm{C}$ is similarly charge to a potential difference $2 \mathrm{~V}$. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is