Explanation:
: Given that,
Capacitance, $\mathrm{C}_{1}=2 \mu \mathrm{F}$
Capacitance, $\mathrm{C}_{2}=3 \mu \mathrm{F}$
Voltage, $\mathrm{V}_{1}=1000 \mathrm{~V}$
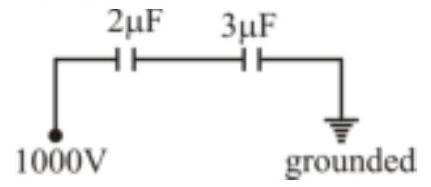
Equivalent Capacitance, $\frac{1}{\mathrm{C}_{\mathrm{eq}}}=\frac{1}{2 \mu \mathrm{F}}+\frac{1}{3 \mu \mathrm{F}}$
$\mathrm{C}_{\mathrm{eq}}=\frac{6}{5} \mu \mathrm{F}$
Charge, $\mathrm{Q}$ on each plate $=\mathrm{C}_{\mathrm{eq}} \cdot \mathrm{V}_{1}$
$=\frac{6}{5} \times 1000 \times 10^{-6}$
$Q =1200 \mu \mathrm{C}$
Potential on inner plate,
$\mathrm{V}=\mathrm{V}_{1}-\frac{\mathrm{Q}}{\mathrm{C}}$
$=1000-\frac{\mathrm{Q}}{\mathrm{C}}$
$=1000-\frac{1200 \mu \mathrm{C}}{2 \mu \mathrm{F}}$
$=1000-600$
$\mathrm{~V} =400 \mathrm{~V}$