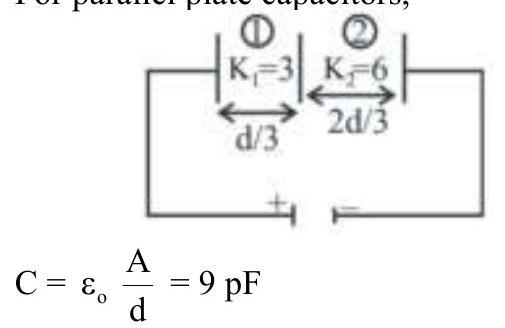
165603 A parallel plate capacitor with air between the plates has a capacitance of $9 \mathrm{pF}$. The separation between the plates is $d$. The space between the plates is now filled with two dielectrics constant $K_{1}=3$ and thickness $d / 3$ while the other one has dielectric constant $K_{2}=$ 6 and thickness 2d/3. Capacitance of the capacitor is now
165603 A parallel plate capacitor with air between the plates has a capacitance of $9 \mathrm{pF}$. The separation between the plates is $d$. The space between the plates is now filled with two dielectrics constant $K_{1}=3$ and thickness $d / 3$ while the other one has dielectric constant $K_{2}=$ 6 and thickness 2d/3. Capacitance of the capacitor is now
165603 A parallel plate capacitor with air between the plates has a capacitance of $9 \mathrm{pF}$. The separation between the plates is $d$. The space between the plates is now filled with two dielectrics constant $K_{1}=3$ and thickness $d / 3$ while the other one has dielectric constant $K_{2}=$ 6 and thickness 2d/3. Capacitance of the capacitor is now
165603 A parallel plate capacitor with air between the plates has a capacitance of $9 \mathrm{pF}$. The separation between the plates is $d$. The space between the plates is now filled with two dielectrics constant $K_{1}=3$ and thickness $d / 3$ while the other one has dielectric constant $K_{2}=$ 6 and thickness 2d/3. Capacitance of the capacitor is now