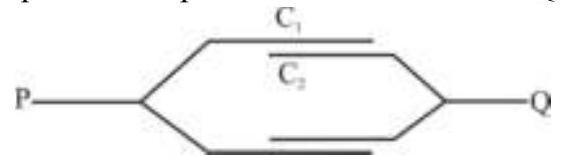
165605 Spherical capacitors has outer sphere of radius $5 \mathrm{~cm}$ and inner sphere of radius $2 \mathrm{~cm}$. when the inner sphere is earthed, its capacity is $C_{1}$ and when the outer sphere is earthed its capacity is $\mathrm{C}_{2}$. Then $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}$ is

165606 27 small drops each having charge $q$ and radius $r$ coalesce to form big drop. How many times charge and capacitance will become?

165607 $\quad$ Figure below shows four plates each of area $A$ and separated from one another by a distance $d$. What is the capacitance between $P$ and $Q$ ?

165608 The capacitance of a spherical conductor with radius $1 \mathrm{~m}$ is

165609 In the figure, charge and the potential difference across the $4 \mu \mathrm{F}$ capacitor will be nearly

165605 Spherical capacitors has outer sphere of radius $5 \mathrm{~cm}$ and inner sphere of radius $2 \mathrm{~cm}$. when the inner sphere is earthed, its capacity is $C_{1}$ and when the outer sphere is earthed its capacity is $\mathrm{C}_{2}$. Then $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}$ is

165606 27 small drops each having charge $q$ and radius $r$ coalesce to form big drop. How many times charge and capacitance will become?

165607 $\quad$ Figure below shows four plates each of area $A$ and separated from one another by a distance $d$. What is the capacitance between $P$ and $Q$ ?

165608 The capacitance of a spherical conductor with radius $1 \mathrm{~m}$ is

165609 In the figure, charge and the potential difference across the $4 \mu \mathrm{F}$ capacitor will be nearly

165605 Spherical capacitors has outer sphere of radius $5 \mathrm{~cm}$ and inner sphere of radius $2 \mathrm{~cm}$. when the inner sphere is earthed, its capacity is $C_{1}$ and when the outer sphere is earthed its capacity is $\mathrm{C}_{2}$. Then $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}$ is

165606 27 small drops each having charge $q$ and radius $r$ coalesce to form big drop. How many times charge and capacitance will become?

165607 $\quad$ Figure below shows four plates each of area $A$ and separated from one another by a distance $d$. What is the capacitance between $P$ and $Q$ ?

165608 The capacitance of a spherical conductor with radius $1 \mathrm{~m}$ is

165609 In the figure, charge and the potential difference across the $4 \mu \mathrm{F}$ capacitor will be nearly

165605 Spherical capacitors has outer sphere of radius $5 \mathrm{~cm}$ and inner sphere of radius $2 \mathrm{~cm}$. when the inner sphere is earthed, its capacity is $C_{1}$ and when the outer sphere is earthed its capacity is $\mathrm{C}_{2}$. Then $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}$ is

165606 27 small drops each having charge $q$ and radius $r$ coalesce to form big drop. How many times charge and capacitance will become?

165607 $\quad$ Figure below shows four plates each of area $A$ and separated from one another by a distance $d$. What is the capacitance between $P$ and $Q$ ?

165608 The capacitance of a spherical conductor with radius $1 \mathrm{~m}$ is

165609 In the figure, charge and the potential difference across the $4 \mu \mathrm{F}$ capacitor will be nearly

165605 Spherical capacitors has outer sphere of radius $5 \mathrm{~cm}$ and inner sphere of radius $2 \mathrm{~cm}$. when the inner sphere is earthed, its capacity is $C_{1}$ and when the outer sphere is earthed its capacity is $\mathrm{C}_{2}$. Then $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}$ is

165606 27 small drops each having charge $q$ and radius $r$ coalesce to form big drop. How many times charge and capacitance will become?

165607 $\quad$ Figure below shows four plates each of area $A$ and separated from one another by a distance $d$. What is the capacitance between $P$ and $Q$ ?

165608 The capacitance of a spherical conductor with radius $1 \mathrm{~m}$ is

165609 In the figure, charge and the potential difference across the $4 \mu \mathrm{F}$ capacitor will be nearly