142312 The work function of a metal is $2 \mathrm{eV}$. If a radiation of wavelength 30000 ss incident on it, the maximum kinetic energy of the emitted photoelectrons is (Planck's constant $h=6.6 \times$ $10^{-34} \mathrm{Js}$; velocity of light $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s} ; 1 \mathrm{eV}=$ $1.6 \times 10^{-19} \mathrm{~J}$ )
142314
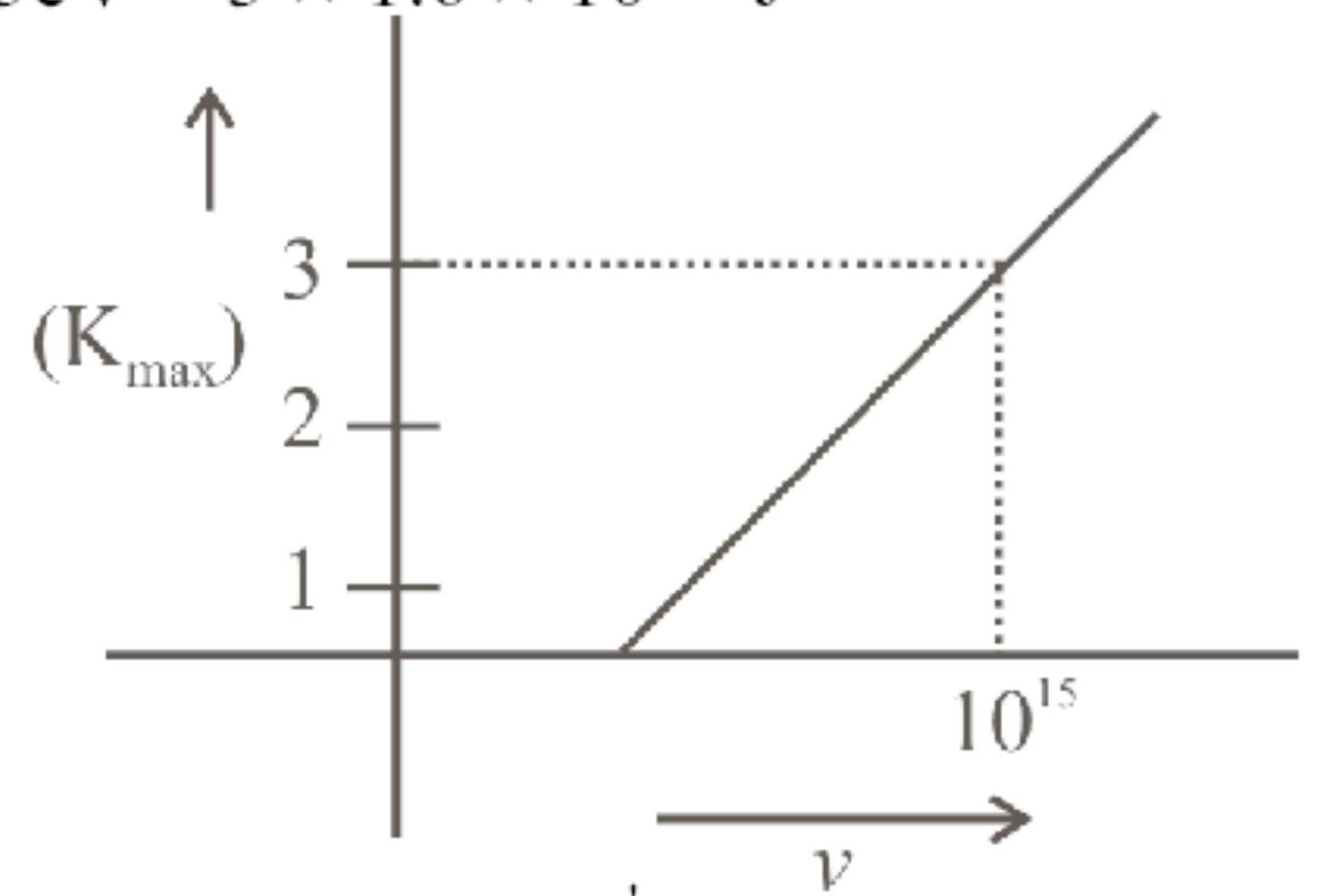
Figure represents a graph of kinetic energy of most energetic photoelectrons, $K_{\max }$ (in $\mathrm{eV}$ ), and frequency (v) for a metal used as cathode in photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is: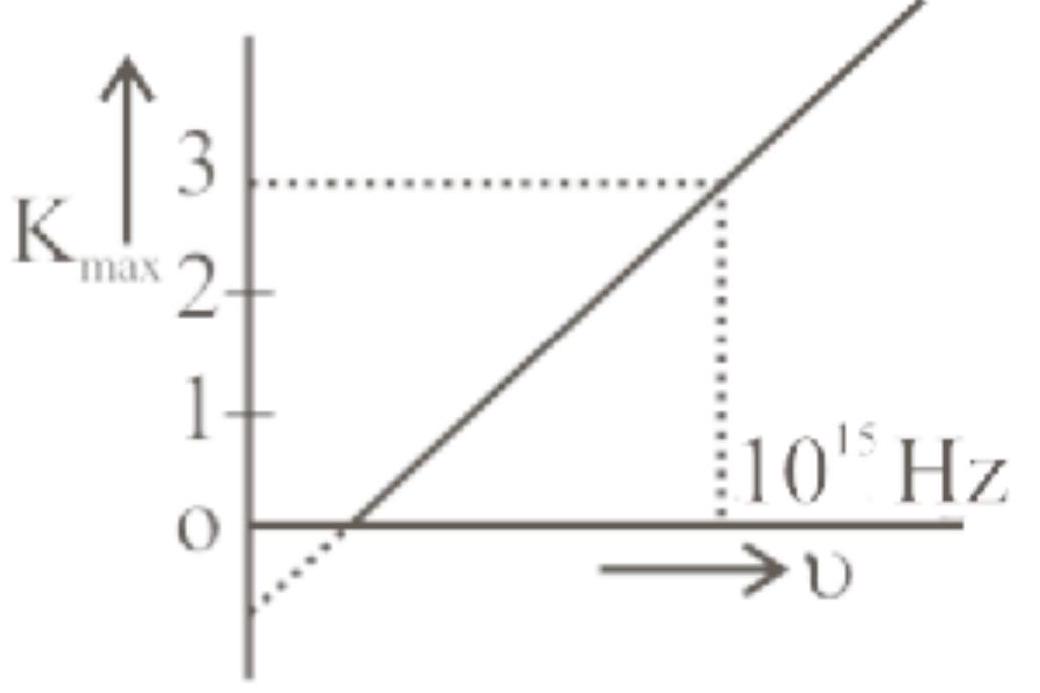
142312 The work function of a metal is $2 \mathrm{eV}$. If a radiation of wavelength 30000 ss incident on it, the maximum kinetic energy of the emitted photoelectrons is (Planck's constant $h=6.6 \times$ $10^{-34} \mathrm{Js}$; velocity of light $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s} ; 1 \mathrm{eV}=$ $1.6 \times 10^{-19} \mathrm{~J}$ )
142314
Figure represents a graph of kinetic energy of most energetic photoelectrons, $K_{\max }$ (in $\mathrm{eV}$ ), and frequency (v) for a metal used as cathode in photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is:
142312 The work function of a metal is $2 \mathrm{eV}$. If a radiation of wavelength 30000 ss incident on it, the maximum kinetic energy of the emitted photoelectrons is (Planck's constant $h=6.6 \times$ $10^{-34} \mathrm{Js}$; velocity of light $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s} ; 1 \mathrm{eV}=$ $1.6 \times 10^{-19} \mathrm{~J}$ )
142314
Figure represents a graph of kinetic energy of most energetic photoelectrons, $K_{\max }$ (in $\mathrm{eV}$ ), and frequency (v) for a metal used as cathode in photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is:
142312 The work function of a metal is $2 \mathrm{eV}$. If a radiation of wavelength 30000 ss incident on it, the maximum kinetic energy of the emitted photoelectrons is (Planck's constant $h=6.6 \times$ $10^{-34} \mathrm{Js}$; velocity of light $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s} ; 1 \mathrm{eV}=$ $1.6 \times 10^{-19} \mathrm{~J}$ )
142314
Figure represents a graph of kinetic energy of most energetic photoelectrons, $K_{\max }$ (in $\mathrm{eV}$ ), and frequency (v) for a metal used as cathode in photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is:
142312 The work function of a metal is $2 \mathrm{eV}$. If a radiation of wavelength 30000 ss incident on it, the maximum kinetic energy of the emitted photoelectrons is (Planck's constant $h=6.6 \times$ $10^{-34} \mathrm{Js}$; velocity of light $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s} ; 1 \mathrm{eV}=$ $1.6 \times 10^{-19} \mathrm{~J}$ )
142314
Figure represents a graph of kinetic energy of most energetic photoelectrons, $K_{\max }$ (in $\mathrm{eV}$ ), and frequency (v) for a metal used as cathode in photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is: