142147
The graph $\frac{1}{\lambda}$ and stopping potential (V) of three metals having work function $\phi_{1}, \phi_{2}$ and $\phi_{3}$ in an experiment of photoelectric effect is plotted as shown in the figure. Which one of the following statement is /are correct? [Here $\lambda$ is the wavelength of the incident rayl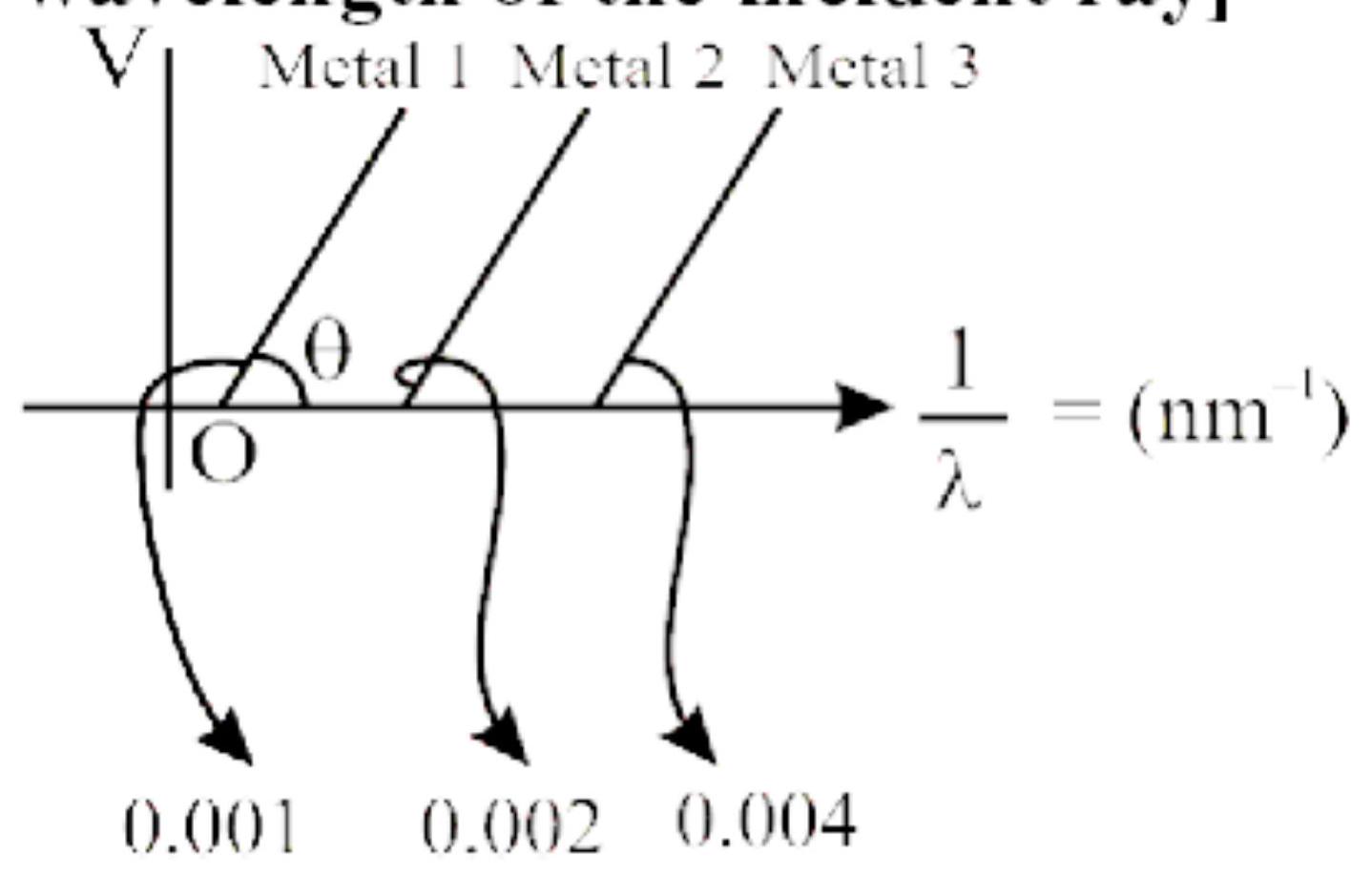
(I) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=1: 2: 4$
(II) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=4: 2: 1$
(III) $\operatorname{Tan} \theta \propto \frac{\mathrm{hc}}{\mathrm{e}}$ where $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ speed of light
(IV) The violet colour-light can eject photoelectrons from metals 2 and 3
142148 Photoelectric emission is observed from a metallic surface for frequency $v_{1}$ and $v_{2}$ of the incident light $\left(v_{1}>v_{2}\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio $1: n$, then the threshold frequency of the metallic surface is
142147
The graph $\frac{1}{\lambda}$ and stopping potential (V) of three metals having work function $\phi_{1}, \phi_{2}$ and $\phi_{3}$ in an experiment of photoelectric effect is plotted as shown in the figure. Which one of the following statement is /are correct? [Here $\lambda$ is the wavelength of the incident rayl
(I) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=1: 2: 4$
(II) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=4: 2: 1$
(III) $\operatorname{Tan} \theta \propto \frac{\mathrm{hc}}{\mathrm{e}}$ where $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ speed of light
(IV) The violet colour-light can eject photoelectrons from metals 2 and 3
142148 Photoelectric emission is observed from a metallic surface for frequency $v_{1}$ and $v_{2}$ of the incident light $\left(v_{1}>v_{2}\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio $1: n$, then the threshold frequency of the metallic surface is
142147
The graph $\frac{1}{\lambda}$ and stopping potential (V) of three metals having work function $\phi_{1}, \phi_{2}$ and $\phi_{3}$ in an experiment of photoelectric effect is plotted as shown in the figure. Which one of the following statement is /are correct? [Here $\lambda$ is the wavelength of the incident rayl
(I) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=1: 2: 4$
(II) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=4: 2: 1$
(III) $\operatorname{Tan} \theta \propto \frac{\mathrm{hc}}{\mathrm{e}}$ where $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ speed of light
(IV) The violet colour-light can eject photoelectrons from metals 2 and 3
142148 Photoelectric emission is observed from a metallic surface for frequency $v_{1}$ and $v_{2}$ of the incident light $\left(v_{1}>v_{2}\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio $1: n$, then the threshold frequency of the metallic surface is
142147
The graph $\frac{1}{\lambda}$ and stopping potential (V) of three metals having work function $\phi_{1}, \phi_{2}$ and $\phi_{3}$ in an experiment of photoelectric effect is plotted as shown in the figure. Which one of the following statement is /are correct? [Here $\lambda$ is the wavelength of the incident rayl
(I) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=1: 2: 4$
(II) Ratio of work functions $\phi_{1}: \phi_{2}: \phi_{3}=4: 2: 1$
(III) $\operatorname{Tan} \theta \propto \frac{\mathrm{hc}}{\mathrm{e}}$ where $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ speed of light
(IV) The violet colour-light can eject photoelectrons from metals 2 and 3
142148 Photoelectric emission is observed from a metallic surface for frequency $v_{1}$ and $v_{2}$ of the incident light $\left(v_{1}>v_{2}\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio $1: n$, then the threshold frequency of the metallic surface is