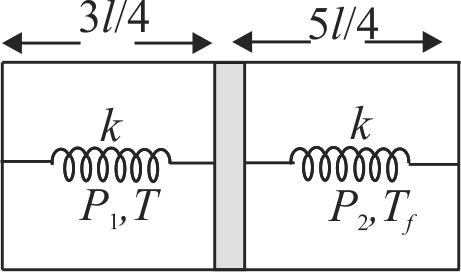
371521 A horizontal insulated cylindrical vessel of length \(2 l\) is separated by a thin insulating piston into two equal parts as shown in fig. Each part contains \(n\) moles of an ideal monoatomic gas at temperature \(T\). The piston is connected to end faces of the cylinder with the help of two springs each of spring constant \(k\). Initially both the springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with the help of filament. If energy (heat) \(Q\) is supplied to right part so that the piston moves to the left by \(\dfrac{l}{4}\), then the change in internal energy of right part of cylinder is: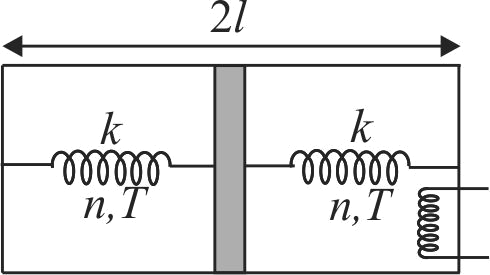

371522 An ideal monoatomic gas in confined in a cylinder by a spring loaded piston of cross section \(8.0 \times {10^{ - 3}}\;{m^2}\). Initially the gas is at \(300\;K\) and occupies a volume of \(2.4 \times {10^{ - 3}}\;{m^3}\) and spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by \(0.1\;m\). The force constant of the spring is \(8000\;N/m\) and the atmospheric pressure is \(1.0 \times {10^5}\;N/{m^2}\). The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be : (Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible):-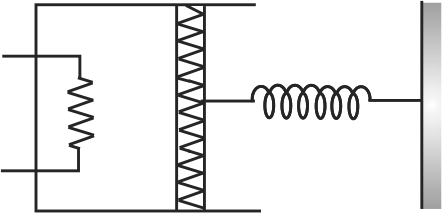

371523 A rectangular box shown in the figure has a partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a monatomic gas \(\left(\gamma=\dfrac{5}{3}\right)\) at a pressure \(P_{0}\), volume \(V_{0}\), and temperature \(T_{0}\). The chamber on the left is slowly heated by an electric heater. The walls of the box and the partition are thermally insulated. Heat loss through the lead wires is negligible. The gas in the left chamber expands, pushing the partition until the final pressure in both chambers becomes \(\dfrac{243\,\, p_{0}}{32}\). If \(P_{0} V_{0}=400 {~J}\), then find the magnitude of work done by the gas in the right chamber.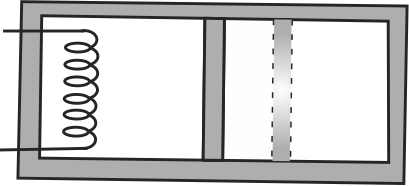

371524 A resistance coil connected to an external battery is placed inside an adiabatic cylinder fitted with a frictionless piston of mass \(m\) and containing an ideal gas. A current \(i\) flows through the coil which has a resistance \(R\). At what speed must the piston move upward in order that the temperature of the gas remains unchanged? Neglect atmospheric pressure.

371521 A horizontal insulated cylindrical vessel of length \(2 l\) is separated by a thin insulating piston into two equal parts as shown in fig. Each part contains \(n\) moles of an ideal monoatomic gas at temperature \(T\). The piston is connected to end faces of the cylinder with the help of two springs each of spring constant \(k\). Initially both the springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with the help of filament. If energy (heat) \(Q\) is supplied to right part so that the piston moves to the left by \(\dfrac{l}{4}\), then the change in internal energy of right part of cylinder is:

371522 An ideal monoatomic gas in confined in a cylinder by a spring loaded piston of cross section \(8.0 \times {10^{ - 3}}\;{m^2}\). Initially the gas is at \(300\;K\) and occupies a volume of \(2.4 \times {10^{ - 3}}\;{m^3}\) and spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by \(0.1\;m\). The force constant of the spring is \(8000\;N/m\) and the atmospheric pressure is \(1.0 \times {10^5}\;N/{m^2}\). The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be : (Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible):-

371523 A rectangular box shown in the figure has a partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a monatomic gas \(\left(\gamma=\dfrac{5}{3}\right)\) at a pressure \(P_{0}\), volume \(V_{0}\), and temperature \(T_{0}\). The chamber on the left is slowly heated by an electric heater. The walls of the box and the partition are thermally insulated. Heat loss through the lead wires is negligible. The gas in the left chamber expands, pushing the partition until the final pressure in both chambers becomes \(\dfrac{243\,\, p_{0}}{32}\). If \(P_{0} V_{0}=400 {~J}\), then find the magnitude of work done by the gas in the right chamber.

371524 A resistance coil connected to an external battery is placed inside an adiabatic cylinder fitted with a frictionless piston of mass \(m\) and containing an ideal gas. A current \(i\) flows through the coil which has a resistance \(R\). At what speed must the piston move upward in order that the temperature of the gas remains unchanged? Neglect atmospheric pressure.

371521 A horizontal insulated cylindrical vessel of length \(2 l\) is separated by a thin insulating piston into two equal parts as shown in fig. Each part contains \(n\) moles of an ideal monoatomic gas at temperature \(T\). The piston is connected to end faces of the cylinder with the help of two springs each of spring constant \(k\). Initially both the springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with the help of filament. If energy (heat) \(Q\) is supplied to right part so that the piston moves to the left by \(\dfrac{l}{4}\), then the change in internal energy of right part of cylinder is:

371522 An ideal monoatomic gas in confined in a cylinder by a spring loaded piston of cross section \(8.0 \times {10^{ - 3}}\;{m^2}\). Initially the gas is at \(300\;K\) and occupies a volume of \(2.4 \times {10^{ - 3}}\;{m^3}\) and spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by \(0.1\;m\). The force constant of the spring is \(8000\;N/m\) and the atmospheric pressure is \(1.0 \times {10^5}\;N/{m^2}\). The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be : (Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible):-

371523 A rectangular box shown in the figure has a partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a monatomic gas \(\left(\gamma=\dfrac{5}{3}\right)\) at a pressure \(P_{0}\), volume \(V_{0}\), and temperature \(T_{0}\). The chamber on the left is slowly heated by an electric heater. The walls of the box and the partition are thermally insulated. Heat loss through the lead wires is negligible. The gas in the left chamber expands, pushing the partition until the final pressure in both chambers becomes \(\dfrac{243\,\, p_{0}}{32}\). If \(P_{0} V_{0}=400 {~J}\), then find the magnitude of work done by the gas in the right chamber.

371524 A resistance coil connected to an external battery is placed inside an adiabatic cylinder fitted with a frictionless piston of mass \(m\) and containing an ideal gas. A current \(i\) flows through the coil which has a resistance \(R\). At what speed must the piston move upward in order that the temperature of the gas remains unchanged? Neglect atmospheric pressure.

371521 A horizontal insulated cylindrical vessel of length \(2 l\) is separated by a thin insulating piston into two equal parts as shown in fig. Each part contains \(n\) moles of an ideal monoatomic gas at temperature \(T\). The piston is connected to end faces of the cylinder with the help of two springs each of spring constant \(k\). Initially both the springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with the help of filament. If energy (heat) \(Q\) is supplied to right part so that the piston moves to the left by \(\dfrac{l}{4}\), then the change in internal energy of right part of cylinder is:

371522 An ideal monoatomic gas in confined in a cylinder by a spring loaded piston of cross section \(8.0 \times {10^{ - 3}}\;{m^2}\). Initially the gas is at \(300\;K\) and occupies a volume of \(2.4 \times {10^{ - 3}}\;{m^3}\) and spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by \(0.1\;m\). The force constant of the spring is \(8000\;N/m\) and the atmospheric pressure is \(1.0 \times {10^5}\;N/{m^2}\). The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be : (Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible):-

371523 A rectangular box shown in the figure has a partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a monatomic gas \(\left(\gamma=\dfrac{5}{3}\right)\) at a pressure \(P_{0}\), volume \(V_{0}\), and temperature \(T_{0}\). The chamber on the left is slowly heated by an electric heater. The walls of the box and the partition are thermally insulated. Heat loss through the lead wires is negligible. The gas in the left chamber expands, pushing the partition until the final pressure in both chambers becomes \(\dfrac{243\,\, p_{0}}{32}\). If \(P_{0} V_{0}=400 {~J}\), then find the magnitude of work done by the gas in the right chamber.

371524 A resistance coil connected to an external battery is placed inside an adiabatic cylinder fitted with a frictionless piston of mass \(m\) and containing an ideal gas. A current \(i\) flows through the coil which has a resistance \(R\). At what speed must the piston move upward in order that the temperature of the gas remains unchanged? Neglect atmospheric pressure.