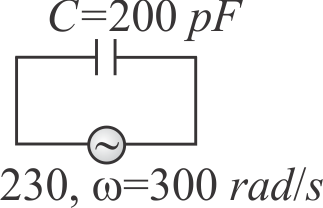
368907
Figure shows a capacitor made of two circular plates each of radius \(12\,cm\), separated by \(5.0\,mm\). The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to \(0.15\,A\), then which of the following is correct?
(Given: \({\varepsilon_{0}=8.85 \times 10^{-12} {C}^{2} N^{-1} {~m}^{-2}}\) )
368907
Figure shows a capacitor made of two circular plates each of radius \(12\,cm\), separated by \(5.0\,mm\). The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to \(0.15\,A\), then which of the following is correct?
(Given: \({\varepsilon_{0}=8.85 \times 10^{-12} {C}^{2} N^{-1} {~m}^{-2}}\) )
368907
Figure shows a capacitor made of two circular plates each of radius \(12\,cm\), separated by \(5.0\,mm\). The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to \(0.15\,A\), then which of the following is correct?
(Given: \({\varepsilon_{0}=8.85 \times 10^{-12} {C}^{2} N^{-1} {~m}^{-2}}\) )
368907
Figure shows a capacitor made of two circular plates each of radius \(12\,cm\), separated by \(5.0\,mm\). The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to \(0.15\,A\), then which of the following is correct?
(Given: \({\varepsilon_{0}=8.85 \times 10^{-12} {C}^{2} N^{-1} {~m}^{-2}}\) )
368907
Figure shows a capacitor made of two circular plates each of radius \(12\,cm\), separated by \(5.0\,mm\). The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to \(0.15\,A\), then which of the following is correct?
(Given: \({\varepsilon_{0}=8.85 \times 10^{-12} {C}^{2} N^{-1} {~m}^{-2}}\) )