368128 In Young's double slit experiment, the wavelength of red light is \(7800\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \) and that of the blue light is \(5200\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \). The value of \(n\) for which \(n^{\text {th }}\) bright band due to red light coincides with \((n+1)^{\text {th }}\) bright band due to blue light, is

368129 If the monochromatic source in Young's double slit experiment is replaced by white light, then

368130 In Young’s double slit experiment, the seventh maximum with wavelength \({\lambda _1}\) is at a distance \({y_1}\) from central maxima and the same maximum with wavelength \({\lambda _2}\) is at distance \({y_2}\) . Then \({y_1}/{y_2}\) :-

368131 White light is used to illuminate two slits in Young's double slit experiment. The separation between the slits is \(b\) and the screen is at a distance \(d(>>b)\) from the slits. At a point on the screen directly in front of one of the slits, which wavelengths are missing?

368128 In Young's double slit experiment, the wavelength of red light is \(7800\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \) and that of the blue light is \(5200\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \). The value of \(n\) for which \(n^{\text {th }}\) bright band due to red light coincides with \((n+1)^{\text {th }}\) bright band due to blue light, is

368129 If the monochromatic source in Young's double slit experiment is replaced by white light, then

368130 In Young’s double slit experiment, the seventh maximum with wavelength \({\lambda _1}\) is at a distance \({y_1}\) from central maxima and the same maximum with wavelength \({\lambda _2}\) is at distance \({y_2}\) . Then \({y_1}/{y_2}\) :-

368131 White light is used to illuminate two slits in Young's double slit experiment. The separation between the slits is \(b\) and the screen is at a distance \(d(>>b)\) from the slits. At a point on the screen directly in front of one of the slits, which wavelengths are missing?

368128 In Young's double slit experiment, the wavelength of red light is \(7800\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \) and that of the blue light is \(5200\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \). The value of \(n\) for which \(n^{\text {th }}\) bright band due to red light coincides with \((n+1)^{\text {th }}\) bright band due to blue light, is

368129 If the monochromatic source in Young's double slit experiment is replaced by white light, then

368130 In Young’s double slit experiment, the seventh maximum with wavelength \({\lambda _1}\) is at a distance \({y_1}\) from central maxima and the same maximum with wavelength \({\lambda _2}\) is at distance \({y_2}\) . Then \({y_1}/{y_2}\) :-

368131 White light is used to illuminate two slits in Young's double slit experiment. The separation between the slits is \(b\) and the screen is at a distance \(d(>>b)\) from the slits. At a point on the screen directly in front of one of the slits, which wavelengths are missing?

368128 In Young's double slit experiment, the wavelength of red light is \(7800\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \) and that of the blue light is \(5200\mathop {{\rm{ }}A}\limits^{\;\;^\circ } \). The value of \(n\) for which \(n^{\text {th }}\) bright band due to red light coincides with \((n+1)^{\text {th }}\) bright band due to blue light, is

368129 If the monochromatic source in Young's double slit experiment is replaced by white light, then

368130 In Young’s double slit experiment, the seventh maximum with wavelength \({\lambda _1}\) is at a distance \({y_1}\) from central maxima and the same maximum with wavelength \({\lambda _2}\) is at distance \({y_2}\) . Then \({y_1}/{y_2}\) :-

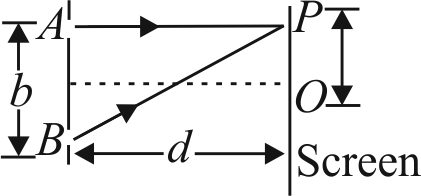
368131 White light is used to illuminate two slits in Young's double slit experiment. The separation between the slits is \(b\) and the screen is at a distance \(d(>>b)\) from the slits. At a point on the screen directly in front of one of the slits, which wavelengths are missing?