368120
Two monochromatic and coherent point sources of light of wavelength \(\lambda \) are placed as shown in the figure below. The initial phase difference between the sources is zero. Select the correct statement \((D > > d).\) If \(d = 4.8\;\lambda \) then total number of minimas on the screen are equal to
368121
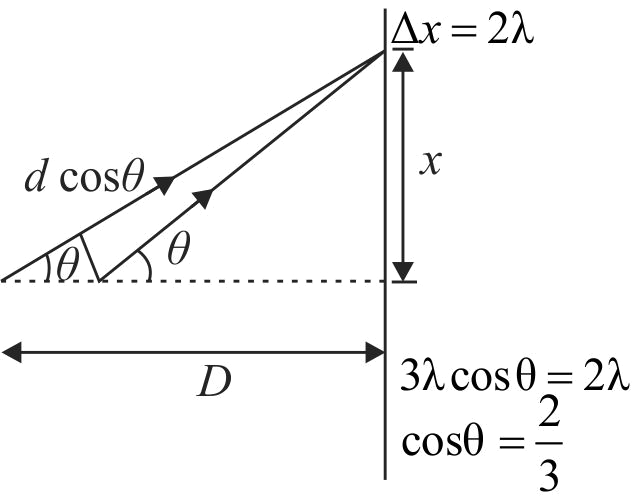
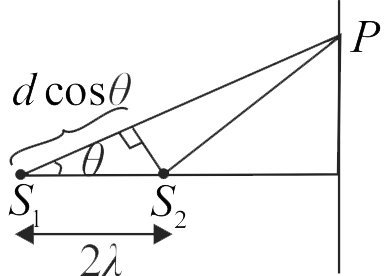
Two coherent narrow slits emitting light of wavelength \(\lambda\) in the same phase are placed parallel to each other at a small seperation of \(3 \lambda\). The light is collected on a screen \(S\) which is placed at a distance \(D(>>\lambda)\) from the slits. The smallest distance \(x\) such that the \(P\) is a maxima.
368122
Assertion :
Two point coherent sources of light \(S_{1}\), and \(S_{2}\) are placed on a line as shown. \(P\) and \(Q\) are two points on that line. If at point \(P\) maximum intensity is observed then maximum intensity should also be observed at \(Q\).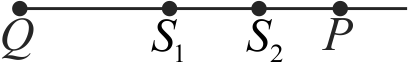
Reason :
In the figure of assertion if the distance \(\left| {{S_1}P - {S_2}P} \right|\) is equal to distance \(\left| {{S_2}Q - {S_1}Q} \right|\) then maximum intensity is observed at both \(P\) and \(Q\).
368123
In Young's double slit experiment, the slits are horizontal. The intensity at a point \({P}\) (as shown in figure) is \(\dfrac{3}{4} I_{m}\), where \(I_{m}\) is the maximum intensity. If the value of \(\theta\) is found to be \(\cos ^{-1}\left(\dfrac{N}{M}\right)\), then the value of \(N+M\) is
368120
Two monochromatic and coherent point sources of light of wavelength \(\lambda \) are placed as shown in the figure below. The initial phase difference between the sources is zero. Select the correct statement \((D > > d).\) If \(d = 4.8\;\lambda \) then total number of minimas on the screen are equal to
368121
Two coherent narrow slits emitting light of wavelength \(\lambda\) in the same phase are placed parallel to each other at a small seperation of \(3 \lambda\). The light is collected on a screen \(S\) which is placed at a distance \(D(>>\lambda)\) from the slits. The smallest distance \(x\) such that the \(P\) is a maxima.
368122
Assertion :
Two point coherent sources of light \(S_{1}\), and \(S_{2}\) are placed on a line as shown. \(P\) and \(Q\) are two points on that line. If at point \(P\) maximum intensity is observed then maximum intensity should also be observed at \(Q\).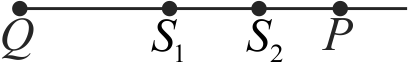
Reason :
In the figure of assertion if the distance \(\left| {{S_1}P - {S_2}P} \right|\) is equal to distance \(\left| {{S_2}Q - {S_1}Q} \right|\) then maximum intensity is observed at both \(P\) and \(Q\).
368123
In Young's double slit experiment, the slits are horizontal. The intensity at a point \({P}\) (as shown in figure) is \(\dfrac{3}{4} I_{m}\), where \(I_{m}\) is the maximum intensity. If the value of \(\theta\) is found to be \(\cos ^{-1}\left(\dfrac{N}{M}\right)\), then the value of \(N+M\) is
368120
Two monochromatic and coherent point sources of light of wavelength \(\lambda \) are placed as shown in the figure below. The initial phase difference between the sources is zero. Select the correct statement \((D > > d).\) If \(d = 4.8\;\lambda \) then total number of minimas on the screen are equal to
368121
Two coherent narrow slits emitting light of wavelength \(\lambda\) in the same phase are placed parallel to each other at a small seperation of \(3 \lambda\). The light is collected on a screen \(S\) which is placed at a distance \(D(>>\lambda)\) from the slits. The smallest distance \(x\) such that the \(P\) is a maxima.
368122
Assertion :
Two point coherent sources of light \(S_{1}\), and \(S_{2}\) are placed on a line as shown. \(P\) and \(Q\) are two points on that line. If at point \(P\) maximum intensity is observed then maximum intensity should also be observed at \(Q\).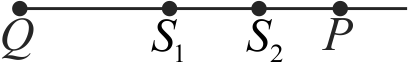
Reason :
In the figure of assertion if the distance \(\left| {{S_1}P - {S_2}P} \right|\) is equal to distance \(\left| {{S_2}Q - {S_1}Q} \right|\) then maximum intensity is observed at both \(P\) and \(Q\).
368123
In Young's double slit experiment, the slits are horizontal. The intensity at a point \({P}\) (as shown in figure) is \(\dfrac{3}{4} I_{m}\), where \(I_{m}\) is the maximum intensity. If the value of \(\theta\) is found to be \(\cos ^{-1}\left(\dfrac{N}{M}\right)\), then the value of \(N+M\) is
368120
Two monochromatic and coherent point sources of light of wavelength \(\lambda \) are placed as shown in the figure below. The initial phase difference between the sources is zero. Select the correct statement \((D > > d).\) If \(d = 4.8\;\lambda \) then total number of minimas on the screen are equal to
368121
Two coherent narrow slits emitting light of wavelength \(\lambda\) in the same phase are placed parallel to each other at a small seperation of \(3 \lambda\). The light is collected on a screen \(S\) which is placed at a distance \(D(>>\lambda)\) from the slits. The smallest distance \(x\) such that the \(P\) is a maxima.
368122
Assertion :
Two point coherent sources of light \(S_{1}\), and \(S_{2}\) are placed on a line as shown. \(P\) and \(Q\) are two points on that line. If at point \(P\) maximum intensity is observed then maximum intensity should also be observed at \(Q\).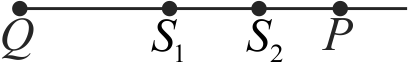
Reason :
In the figure of assertion if the distance \(\left| {{S_1}P - {S_2}P} \right|\) is equal to distance \(\left| {{S_2}Q - {S_1}Q} \right|\) then maximum intensity is observed at both \(P\) and \(Q\).
368123
In Young's double slit experiment, the slits are horizontal. The intensity at a point \({P}\) (as shown in figure) is \(\dfrac{3}{4} I_{m}\), where \(I_{m}\) is the maximum intensity. If the value of \(\theta\) is found to be \(\cos ^{-1}\left(\dfrac{N}{M}\right)\), then the value of \(N+M\) is
368120
Two monochromatic and coherent point sources of light of wavelength \(\lambda \) are placed as shown in the figure below. The initial phase difference between the sources is zero. Select the correct statement \((D > > d).\) If \(d = 4.8\;\lambda \) then total number of minimas on the screen are equal to
368121
Two coherent narrow slits emitting light of wavelength \(\lambda\) in the same phase are placed parallel to each other at a small seperation of \(3 \lambda\). The light is collected on a screen \(S\) which is placed at a distance \(D(>>\lambda)\) from the slits. The smallest distance \(x\) such that the \(P\) is a maxima.
368122
Assertion :
Two point coherent sources of light \(S_{1}\), and \(S_{2}\) are placed on a line as shown. \(P\) and \(Q\) are two points on that line. If at point \(P\) maximum intensity is observed then maximum intensity should also be observed at \(Q\).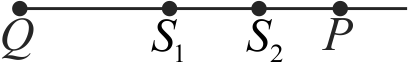
Reason :
In the figure of assertion if the distance \(\left| {{S_1}P - {S_2}P} \right|\) is equal to distance \(\left| {{S_2}Q - {S_1}Q} \right|\) then maximum intensity is observed at both \(P\) and \(Q\).
368123
In Young's double slit experiment, the slits are horizontal. The intensity at a point \({P}\) (as shown in figure) is \(\dfrac{3}{4} I_{m}\), where \(I_{m}\) is the maximum intensity. If the value of \(\theta\) is found to be \(\cos ^{-1}\left(\dfrac{N}{M}\right)\), then the value of \(N+M\) is