368055 In Young's double slit experiment, an electron beam is used to produce interference fringes of width \({\beta_{1}}\). Now the electron beam is replaced by a beam of protons with the same experimental set-up and same speed. The fringe width obtained is \({\beta_{2}}\). The correct relation between \({\beta _1}\) and \({\beta_{2}}\) is

368056 In \(YDSE\) experiment shown in the figure, a parallel beam of light of wavelength \((\lambda = 0.3\;mm)\) in medium \({\mu _1}\) is incident at an angle \(\theta=30^{\circ}\) as shown \(\left(S_{1} O=S_{2} O\right)\). If the intensity due to each light wave at point \(O\) is \(I_{0}\) then the resultant intensity at point \(O\) will be: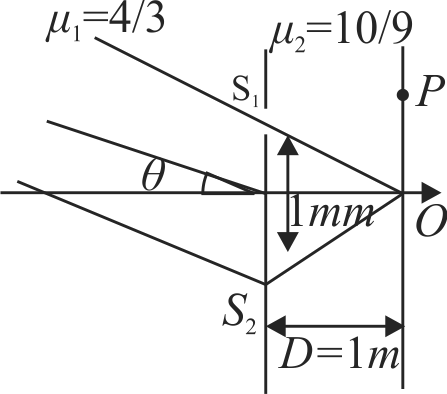

368057 In the Young's double slit experiment, the intensity of light passing through each of the two double slits is \(2 \times {10^{ - 2}}W{m^{ - 2}}\). The screen slit distance is very large in comparison with slit-slit distance. The fringe width is \(\beta\). The distance between the central maximum and a point \(P\) on the screen is \(x=\dfrac{\beta}{3}\). Then the total light intensity at that point is

368058 Figure shows a double slit experiment, \(P\) and \(Q\) are the two coherent sources. The path lengths \(P Y\) and \(Q Y\) are \(n \lambda\) and \((n+4) \lambda\) respectively where \(n\) is whole number and \(\lambda\) is wavelength. Taking the central bright fringe has zero path difference, what is formed at \(Y\) ?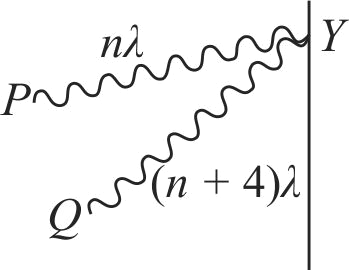

368055 In Young's double slit experiment, an electron beam is used to produce interference fringes of width \({\beta_{1}}\). Now the electron beam is replaced by a beam of protons with the same experimental set-up and same speed. The fringe width obtained is \({\beta_{2}}\). The correct relation between \({\beta _1}\) and \({\beta_{2}}\) is

368056 In \(YDSE\) experiment shown in the figure, a parallel beam of light of wavelength \((\lambda = 0.3\;mm)\) in medium \({\mu _1}\) is incident at an angle \(\theta=30^{\circ}\) as shown \(\left(S_{1} O=S_{2} O\right)\). If the intensity due to each light wave at point \(O\) is \(I_{0}\) then the resultant intensity at point \(O\) will be:

368057 In the Young's double slit experiment, the intensity of light passing through each of the two double slits is \(2 \times {10^{ - 2}}W{m^{ - 2}}\). The screen slit distance is very large in comparison with slit-slit distance. The fringe width is \(\beta\). The distance between the central maximum and a point \(P\) on the screen is \(x=\dfrac{\beta}{3}\). Then the total light intensity at that point is

368058 Figure shows a double slit experiment, \(P\) and \(Q\) are the two coherent sources. The path lengths \(P Y\) and \(Q Y\) are \(n \lambda\) and \((n+4) \lambda\) respectively where \(n\) is whole number and \(\lambda\) is wavelength. Taking the central bright fringe has zero path difference, what is formed at \(Y\) ?

368055 In Young's double slit experiment, an electron beam is used to produce interference fringes of width \({\beta_{1}}\). Now the electron beam is replaced by a beam of protons with the same experimental set-up and same speed. The fringe width obtained is \({\beta_{2}}\). The correct relation between \({\beta _1}\) and \({\beta_{2}}\) is

368056 In \(YDSE\) experiment shown in the figure, a parallel beam of light of wavelength \((\lambda = 0.3\;mm)\) in medium \({\mu _1}\) is incident at an angle \(\theta=30^{\circ}\) as shown \(\left(S_{1} O=S_{2} O\right)\). If the intensity due to each light wave at point \(O\) is \(I_{0}\) then the resultant intensity at point \(O\) will be:

368057 In the Young's double slit experiment, the intensity of light passing through each of the two double slits is \(2 \times {10^{ - 2}}W{m^{ - 2}}\). The screen slit distance is very large in comparison with slit-slit distance. The fringe width is \(\beta\). The distance between the central maximum and a point \(P\) on the screen is \(x=\dfrac{\beta}{3}\). Then the total light intensity at that point is

368058 Figure shows a double slit experiment, \(P\) and \(Q\) are the two coherent sources. The path lengths \(P Y\) and \(Q Y\) are \(n \lambda\) and \((n+4) \lambda\) respectively where \(n\) is whole number and \(\lambda\) is wavelength. Taking the central bright fringe has zero path difference, what is formed at \(Y\) ?

368055 In Young's double slit experiment, an electron beam is used to produce interference fringes of width \({\beta_{1}}\). Now the electron beam is replaced by a beam of protons with the same experimental set-up and same speed. The fringe width obtained is \({\beta_{2}}\). The correct relation between \({\beta _1}\) and \({\beta_{2}}\) is

368056 In \(YDSE\) experiment shown in the figure, a parallel beam of light of wavelength \((\lambda = 0.3\;mm)\) in medium \({\mu _1}\) is incident at an angle \(\theta=30^{\circ}\) as shown \(\left(S_{1} O=S_{2} O\right)\). If the intensity due to each light wave at point \(O\) is \(I_{0}\) then the resultant intensity at point \(O\) will be:

368057 In the Young's double slit experiment, the intensity of light passing through each of the two double slits is \(2 \times {10^{ - 2}}W{m^{ - 2}}\). The screen slit distance is very large in comparison with slit-slit distance. The fringe width is \(\beta\). The distance between the central maximum and a point \(P\) on the screen is \(x=\dfrac{\beta}{3}\). Then the total light intensity at that point is

368058 Figure shows a double slit experiment, \(P\) and \(Q\) are the two coherent sources. The path lengths \(P Y\) and \(Q Y\) are \(n \lambda\) and \((n+4) \lambda\) respectively where \(n\) is whole number and \(\lambda\) is wavelength. Taking the central bright fringe has zero path difference, what is formed at \(Y\) ?