368011
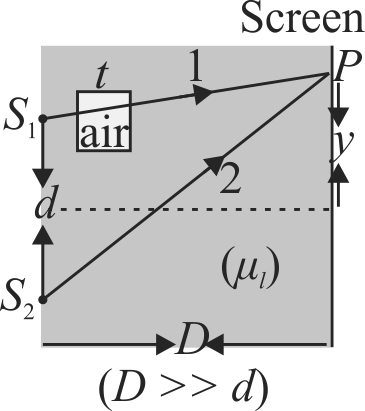
A screen is at a distance 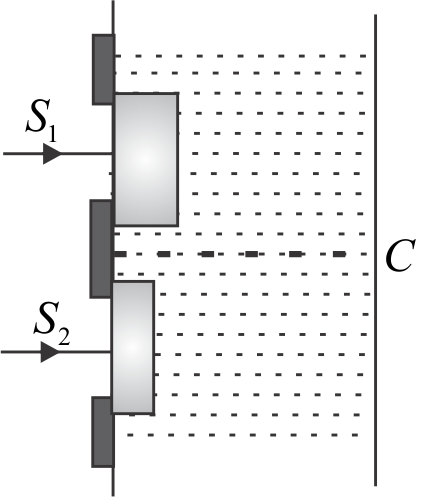
368014
In Young's double slit experiment the two slits are illuminated by light of wavelength 5890
368011
A screen is at a distance 
368014
In Young's double slit experiment the two slits are illuminated by light of wavelength 5890
368011
A screen is at a distance 
368014
In Young's double slit experiment the two slits are illuminated by light of wavelength 5890
368011
A screen is at a distance 
368014
In Young's double slit experiment the two slits are illuminated by light of wavelength 5890
368011
A screen is at a distance 
368014
In Young's double slit experiment the two slits are illuminated by light of wavelength 5890