368103
Two identical narrow slits \(S_{1}\) and \(S_{2}\) are illuminated by light of wavelength \(\lambda\) from a point source \(P\). An interference pattern is produced on the screen as shown in figure. The condition for destructive interference at \(Q\) is that ( \(n\) is an integer)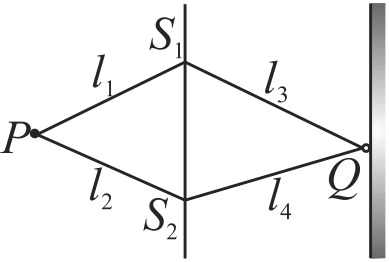
368103
Two identical narrow slits \(S_{1}\) and \(S_{2}\) are illuminated by light of wavelength \(\lambda\) from a point source \(P\). An interference pattern is produced on the screen as shown in figure. The condition for destructive interference at \(Q\) is that ( \(n\) is an integer)
368103
Two identical narrow slits \(S_{1}\) and \(S_{2}\) are illuminated by light of wavelength \(\lambda\) from a point source \(P\). An interference pattern is produced on the screen as shown in figure. The condition for destructive interference at \(Q\) is that ( \(n\) is an integer)
368103
Two identical narrow slits \(S_{1}\) and \(S_{2}\) are illuminated by light of wavelength \(\lambda\) from a point source \(P\). An interference pattern is produced on the screen as shown in figure. The condition for destructive interference at \(Q\) is that ( \(n\) is an integer)
368103
Two identical narrow slits \(S_{1}\) and \(S_{2}\) are illuminated by light of wavelength \(\lambda\) from a point source \(P\). An interference pattern is produced on the screen as shown in figure. The condition for destructive interference at \(Q\) is that ( \(n\) is an integer)