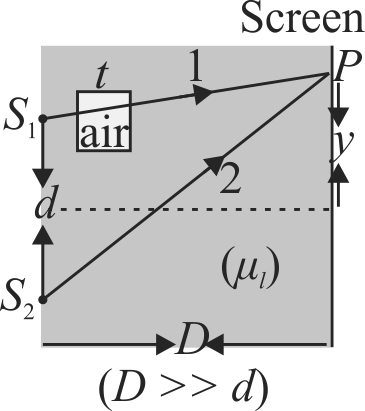
368011
A screen is at a distance \({D}=80 {~cm}\) from a diaphragm having two narrow slits \({S}_{1}\) and \({S}_{2}\) which are \({d}=2 {~mm}\) apart. Slit \({S}_{1}\) is covered by a transparent sheet of thickness \(t_{1}=2.5 \,\mu {m}\) and slit \({S}_{2}\) is covered by another sheet of thickness \({t}_{2}=1.25 \mu {m}\). (as in figure). Both sheets are made of same material having refractive index \(\mu_{{s}}=1.40\). Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength \(\lambda = 5000\)\( \mathop A^{~~\circ} \) is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate the ratio of intensity of \({C}\) to maximum intensity of interference pattern obtained on the screen \(\left(\mu_{{w}}=\dfrac{4}{3}\right)\).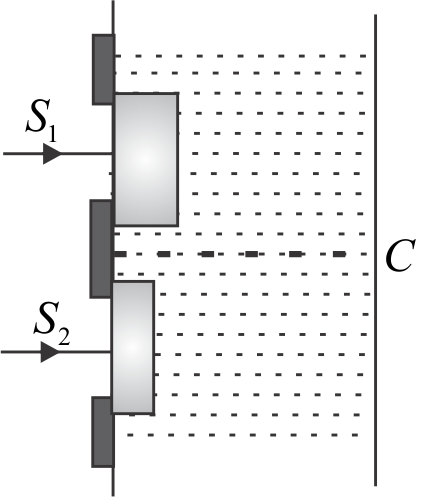
368012 A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of \(1\;mm\) and distance between the plane of slits and screen \(1.33\;m\). The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\( \mathop A^{~~\circ} \). The fringe width is:
368014 In Young's double slit experiment the two slits are illuminated by light of wavelength 5890 \( \mathop A^{~~\circ} \) and the angular distance between any two consecutive bright fringes obtained on the screen is \(0.2^{\circ}\). if the whole apparatus is immersed in water then the angular fringe width will be, (if the refractive index of water is \(4 / 3\) ):
368011
A screen is at a distance \({D}=80 {~cm}\) from a diaphragm having two narrow slits \({S}_{1}\) and \({S}_{2}\) which are \({d}=2 {~mm}\) apart. Slit \({S}_{1}\) is covered by a transparent sheet of thickness \(t_{1}=2.5 \,\mu {m}\) and slit \({S}_{2}\) is covered by another sheet of thickness \({t}_{2}=1.25 \mu {m}\). (as in figure). Both sheets are made of same material having refractive index \(\mu_{{s}}=1.40\). Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength \(\lambda = 5000\)\( \mathop A^{~~\circ} \) is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate the ratio of intensity of \({C}\) to maximum intensity of interference pattern obtained on the screen \(\left(\mu_{{w}}=\dfrac{4}{3}\right)\).
368012 A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of \(1\;mm\) and distance between the plane of slits and screen \(1.33\;m\). The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\( \mathop A^{~~\circ} \). The fringe width is:
368014 In Young's double slit experiment the two slits are illuminated by light of wavelength 5890 \( \mathop A^{~~\circ} \) and the angular distance between any two consecutive bright fringes obtained on the screen is \(0.2^{\circ}\). if the whole apparatus is immersed in water then the angular fringe width will be, (if the refractive index of water is \(4 / 3\) ):
368011
A screen is at a distance \({D}=80 {~cm}\) from a diaphragm having two narrow slits \({S}_{1}\) and \({S}_{2}\) which are \({d}=2 {~mm}\) apart. Slit \({S}_{1}\) is covered by a transparent sheet of thickness \(t_{1}=2.5 \,\mu {m}\) and slit \({S}_{2}\) is covered by another sheet of thickness \({t}_{2}=1.25 \mu {m}\). (as in figure). Both sheets are made of same material having refractive index \(\mu_{{s}}=1.40\). Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength \(\lambda = 5000\)\( \mathop A^{~~\circ} \) is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate the ratio of intensity of \({C}\) to maximum intensity of interference pattern obtained on the screen \(\left(\mu_{{w}}=\dfrac{4}{3}\right)\).
368012 A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of \(1\;mm\) and distance between the plane of slits and screen \(1.33\;m\). The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\( \mathop A^{~~\circ} \). The fringe width is:
368014 In Young's double slit experiment the two slits are illuminated by light of wavelength 5890 \( \mathop A^{~~\circ} \) and the angular distance between any two consecutive bright fringes obtained on the screen is \(0.2^{\circ}\). if the whole apparatus is immersed in water then the angular fringe width will be, (if the refractive index of water is \(4 / 3\) ):
368011
A screen is at a distance \({D}=80 {~cm}\) from a diaphragm having two narrow slits \({S}_{1}\) and \({S}_{2}\) which are \({d}=2 {~mm}\) apart. Slit \({S}_{1}\) is covered by a transparent sheet of thickness \(t_{1}=2.5 \,\mu {m}\) and slit \({S}_{2}\) is covered by another sheet of thickness \({t}_{2}=1.25 \mu {m}\). (as in figure). Both sheets are made of same material having refractive index \(\mu_{{s}}=1.40\). Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength \(\lambda = 5000\)\( \mathop A^{~~\circ} \) is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate the ratio of intensity of \({C}\) to maximum intensity of interference pattern obtained on the screen \(\left(\mu_{{w}}=\dfrac{4}{3}\right)\).
368012 A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of \(1\;mm\) and distance between the plane of slits and screen \(1.33\;m\). The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\( \mathop A^{~~\circ} \). The fringe width is:
368014 In Young's double slit experiment the two slits are illuminated by light of wavelength 5890 \( \mathop A^{~~\circ} \) and the angular distance between any two consecutive bright fringes obtained on the screen is \(0.2^{\circ}\). if the whole apparatus is immersed in water then the angular fringe width will be, (if the refractive index of water is \(4 / 3\) ):
368011
A screen is at a distance \({D}=80 {~cm}\) from a diaphragm having two narrow slits \({S}_{1}\) and \({S}_{2}\) which are \({d}=2 {~mm}\) apart. Slit \({S}_{1}\) is covered by a transparent sheet of thickness \(t_{1}=2.5 \,\mu {m}\) and slit \({S}_{2}\) is covered by another sheet of thickness \({t}_{2}=1.25 \mu {m}\). (as in figure). Both sheets are made of same material having refractive index \(\mu_{{s}}=1.40\). Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength \(\lambda = 5000\)\( \mathop A^{~~\circ} \) is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate the ratio of intensity of \({C}\) to maximum intensity of interference pattern obtained on the screen \(\left(\mu_{{w}}=\dfrac{4}{3}\right)\).
368012 A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of \(1\;mm\) and distance between the plane of slits and screen \(1.33\;m\). The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\( \mathop A^{~~\circ} \). The fringe width is:
368014 In Young's double slit experiment the two slits are illuminated by light of wavelength 5890 \( \mathop A^{~~\circ} \) and the angular distance between any two consecutive bright fringes obtained on the screen is \(0.2^{\circ}\). if the whole apparatus is immersed in water then the angular fringe width will be, (if the refractive index of water is \(4 / 3\) ):