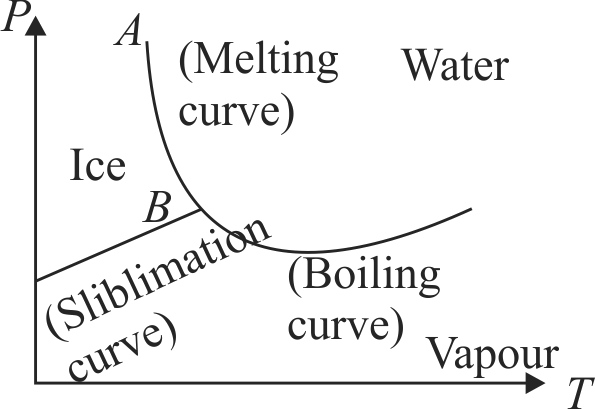
366828 A solid whose volume does not change with temperature floats in a liquid. For two different temperatures \(t_{1}\) and \(t_{2}\) of the liquid, dfractions \(f_{1}\) and \(f_{2}\) of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to

366829 Assertion :
In pressure-temperature \((P-T)\) phase diagram of water, the slope of the melting curve is found to be negative.
Reason :
Ice contracts on melting to water

366830 The coefficient of cubical expansion of mercury is \(0.00018/^\circ C\) and that of brass \(0.00006/^\circ C\). If a barometer having a brass scale were to read \(74.5\;cm\) at \(30^\circ C\), find the true barometric height at\(0^\circ C\). The scale is supposed to be correct at \(15^\circ C\).

366831 As shown in the picture a cylinder with volumetric thermal expansion coefficient of \({\gamma _s} = 3 \times {10^{ - 6}}/^\circ C\) is completely submerged and floating in a fluid at the temperature \(50^\circ C\). The fluid has volumetric thermal expansion coefficient of \({\gamma _l} = 8 \times {10^{ - 5}}/^\circ C\).
If we cool down the cylinder and fluid to \(0^\circ C\) what percentage of the cylinder's height will be out of the fluid?

366828 A solid whose volume does not change with temperature floats in a liquid. For two different temperatures \(t_{1}\) and \(t_{2}\) of the liquid, dfractions \(f_{1}\) and \(f_{2}\) of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to

366829 Assertion :
In pressure-temperature \((P-T)\) phase diagram of water, the slope of the melting curve is found to be negative.
Reason :
Ice contracts on melting to water

366830 The coefficient of cubical expansion of mercury is \(0.00018/^\circ C\) and that of brass \(0.00006/^\circ C\). If a barometer having a brass scale were to read \(74.5\;cm\) at \(30^\circ C\), find the true barometric height at\(0^\circ C\). The scale is supposed to be correct at \(15^\circ C\).

366831 As shown in the picture a cylinder with volumetric thermal expansion coefficient of \({\gamma _s} = 3 \times {10^{ - 6}}/^\circ C\) is completely submerged and floating in a fluid at the temperature \(50^\circ C\). The fluid has volumetric thermal expansion coefficient of \({\gamma _l} = 8 \times {10^{ - 5}}/^\circ C\).
If we cool down the cylinder and fluid to \(0^\circ C\) what percentage of the cylinder's height will be out of the fluid?

366828 A solid whose volume does not change with temperature floats in a liquid. For two different temperatures \(t_{1}\) and \(t_{2}\) of the liquid, dfractions \(f_{1}\) and \(f_{2}\) of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to

366829 Assertion :
In pressure-temperature \((P-T)\) phase diagram of water, the slope of the melting curve is found to be negative.
Reason :
Ice contracts on melting to water

366830 The coefficient of cubical expansion of mercury is \(0.00018/^\circ C\) and that of brass \(0.00006/^\circ C\). If a barometer having a brass scale were to read \(74.5\;cm\) at \(30^\circ C\), find the true barometric height at\(0^\circ C\). The scale is supposed to be correct at \(15^\circ C\).

366831 As shown in the picture a cylinder with volumetric thermal expansion coefficient of \({\gamma _s} = 3 \times {10^{ - 6}}/^\circ C\) is completely submerged and floating in a fluid at the temperature \(50^\circ C\). The fluid has volumetric thermal expansion coefficient of \({\gamma _l} = 8 \times {10^{ - 5}}/^\circ C\).
If we cool down the cylinder and fluid to \(0^\circ C\) what percentage of the cylinder's height will be out of the fluid?

366828 A solid whose volume does not change with temperature floats in a liquid. For two different temperatures \(t_{1}\) and \(t_{2}\) of the liquid, dfractions \(f_{1}\) and \(f_{2}\) of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to

366829 Assertion :
In pressure-temperature \((P-T)\) phase diagram of water, the slope of the melting curve is found to be negative.
Reason :
Ice contracts on melting to water

366830 The coefficient of cubical expansion of mercury is \(0.00018/^\circ C\) and that of brass \(0.00006/^\circ C\). If a barometer having a brass scale were to read \(74.5\;cm\) at \(30^\circ C\), find the true barometric height at\(0^\circ C\). The scale is supposed to be correct at \(15^\circ C\).

366831 As shown in the picture a cylinder with volumetric thermal expansion coefficient of \({\gamma _s} = 3 \times {10^{ - 6}}/^\circ C\) is completely submerged and floating in a fluid at the temperature \(50^\circ C\). The fluid has volumetric thermal expansion coefficient of \({\gamma _l} = 8 \times {10^{ - 5}}/^\circ C\).
If we cool down the cylinder and fluid to \(0^\circ C\) what percentage of the cylinder's height will be out of the fluid?