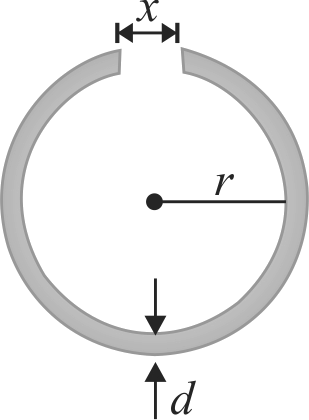
366756 The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula \(\alpha=a T\), where \(a\) is a positive constant and \(T\) in \(^\circ C\). If the length of the rod is \(l\) at temperature \(0^\circ C\), then the temperature at which the length will be \(2 l\) is:
366758
What should be the lengths of a steel and copper rod at \(0^\circ C\) so that the length of the steel rod is \(5\;cm\) longer than the copper rod at any temperature
\(\alpha \,\left( {Steel} \right){\rm{ }} = 1.1 \times {10^{ - 5}}\,^\circ {C^{ - 1}}\) Copper \( = 1.7 \times {10^{ - 5}}\,^\circ C\)
366756 The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula \(\alpha=a T\), where \(a\) is a positive constant and \(T\) in \(^\circ C\). If the length of the rod is \(l\) at temperature \(0^\circ C\), then the temperature at which the length will be \(2 l\) is:
366758
What should be the lengths of a steel and copper rod at \(0^\circ C\) so that the length of the steel rod is \(5\;cm\) longer than the copper rod at any temperature
\(\alpha \,\left( {Steel} \right){\rm{ }} = 1.1 \times {10^{ - 5}}\,^\circ {C^{ - 1}}\) Copper \( = 1.7 \times {10^{ - 5}}\,^\circ C\)
366756 The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula \(\alpha=a T\), where \(a\) is a positive constant and \(T\) in \(^\circ C\). If the length of the rod is \(l\) at temperature \(0^\circ C\), then the temperature at which the length will be \(2 l\) is:
366758
What should be the lengths of a steel and copper rod at \(0^\circ C\) so that the length of the steel rod is \(5\;cm\) longer than the copper rod at any temperature
\(\alpha \,\left( {Steel} \right){\rm{ }} = 1.1 \times {10^{ - 5}}\,^\circ {C^{ - 1}}\) Copper \( = 1.7 \times {10^{ - 5}}\,^\circ C\)
366756 The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula \(\alpha=a T\), where \(a\) is a positive constant and \(T\) in \(^\circ C\). If the length of the rod is \(l\) at temperature \(0^\circ C\), then the temperature at which the length will be \(2 l\) is:
366758
What should be the lengths of a steel and copper rod at \(0^\circ C\) so that the length of the steel rod is \(5\;cm\) longer than the copper rod at any temperature
\(\alpha \,\left( {Steel} \right){\rm{ }} = 1.1 \times {10^{ - 5}}\,^\circ {C^{ - 1}}\) Copper \( = 1.7 \times {10^{ - 5}}\,^\circ C\)