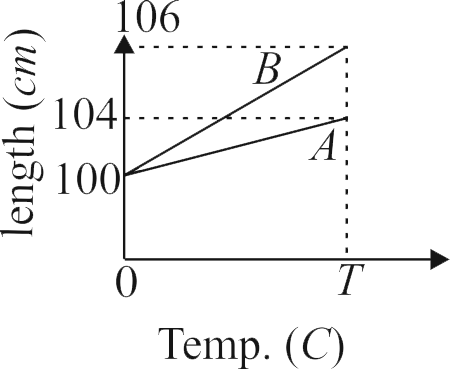
366746 The wooden wheel of radius \(R\) is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area \(S\) and length \(L . L\) is slightly less than \(2 \pi R\). To fit the ring on the wheel, it is heated so that its temperature rises by \(\Delta T\) and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is \(\alpha\) and its Young's modulus is \(Y\), the force that one part of the wheel applies on the other part is

366747 The variation of lengths of two metal rods \({A}\) and \({B}\) with change in temperature is shown in the figure. The ratio of \({\dfrac{\alpha_{A}}{\alpha_{B}}}\) is

366748 Two rods, one of aluminium and the other made of steel, having initial length \(l_{1}\) and \(l_{2}\) are connected together to form a single rod of length \(l_{1}+l_{2}\). The coefficients of linear expansion for aluminium and steel are \(\alpha_{a}\) and \(\alpha_{s}\) respectively. If the length of each rod increase by the same amount when their temperature is raised by \(t^\circ C\), then find the ratio \(\dfrac{l_{1}}{\left(l_{1}+l_{2}\right)}\)

366749 A metallic tape gives correct value at \(25^\circ C\). A piece of wood is being meassured by this metallic tape at \(10^\circ C\). The reading is \(30\;cm\) on the tape, the real length of wooden piece must be

366750 Coefficient of linear expansion of brass and steel rods are \(\alpha_{1}\) and \(\alpha_{2}\). Lengths of brass and steel rods are \(\ell_{1}\) and \(\ell_{2}\) respectively. If \(\left(\ell_{2}-\ell_{1}\right)\) is maintained same at all temperatures, which one of the following relations holds good?

366746 The wooden wheel of radius \(R\) is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area \(S\) and length \(L . L\) is slightly less than \(2 \pi R\). To fit the ring on the wheel, it is heated so that its temperature rises by \(\Delta T\) and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is \(\alpha\) and its Young's modulus is \(Y\), the force that one part of the wheel applies on the other part is

366747 The variation of lengths of two metal rods \({A}\) and \({B}\) with change in temperature is shown in the figure. The ratio of \({\dfrac{\alpha_{A}}{\alpha_{B}}}\) is

366748 Two rods, one of aluminium and the other made of steel, having initial length \(l_{1}\) and \(l_{2}\) are connected together to form a single rod of length \(l_{1}+l_{2}\). The coefficients of linear expansion for aluminium and steel are \(\alpha_{a}\) and \(\alpha_{s}\) respectively. If the length of each rod increase by the same amount when their temperature is raised by \(t^\circ C\), then find the ratio \(\dfrac{l_{1}}{\left(l_{1}+l_{2}\right)}\)

366749 A metallic tape gives correct value at \(25^\circ C\). A piece of wood is being meassured by this metallic tape at \(10^\circ C\). The reading is \(30\;cm\) on the tape, the real length of wooden piece must be

366750 Coefficient of linear expansion of brass and steel rods are \(\alpha_{1}\) and \(\alpha_{2}\). Lengths of brass and steel rods are \(\ell_{1}\) and \(\ell_{2}\) respectively. If \(\left(\ell_{2}-\ell_{1}\right)\) is maintained same at all temperatures, which one of the following relations holds good?

366746 The wooden wheel of radius \(R\) is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area \(S\) and length \(L . L\) is slightly less than \(2 \pi R\). To fit the ring on the wheel, it is heated so that its temperature rises by \(\Delta T\) and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is \(\alpha\) and its Young's modulus is \(Y\), the force that one part of the wheel applies on the other part is

366747 The variation of lengths of two metal rods \({A}\) and \({B}\) with change in temperature is shown in the figure. The ratio of \({\dfrac{\alpha_{A}}{\alpha_{B}}}\) is

366748 Two rods, one of aluminium and the other made of steel, having initial length \(l_{1}\) and \(l_{2}\) are connected together to form a single rod of length \(l_{1}+l_{2}\). The coefficients of linear expansion for aluminium and steel are \(\alpha_{a}\) and \(\alpha_{s}\) respectively. If the length of each rod increase by the same amount when their temperature is raised by \(t^\circ C\), then find the ratio \(\dfrac{l_{1}}{\left(l_{1}+l_{2}\right)}\)

366749 A metallic tape gives correct value at \(25^\circ C\). A piece of wood is being meassured by this metallic tape at \(10^\circ C\). The reading is \(30\;cm\) on the tape, the real length of wooden piece must be

366750 Coefficient of linear expansion of brass and steel rods are \(\alpha_{1}\) and \(\alpha_{2}\). Lengths of brass and steel rods are \(\ell_{1}\) and \(\ell_{2}\) respectively. If \(\left(\ell_{2}-\ell_{1}\right)\) is maintained same at all temperatures, which one of the following relations holds good?

366746 The wooden wheel of radius \(R\) is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area \(S\) and length \(L . L\) is slightly less than \(2 \pi R\). To fit the ring on the wheel, it is heated so that its temperature rises by \(\Delta T\) and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is \(\alpha\) and its Young's modulus is \(Y\), the force that one part of the wheel applies on the other part is

366747 The variation of lengths of two metal rods \({A}\) and \({B}\) with change in temperature is shown in the figure. The ratio of \({\dfrac{\alpha_{A}}{\alpha_{B}}}\) is

366748 Two rods, one of aluminium and the other made of steel, having initial length \(l_{1}\) and \(l_{2}\) are connected together to form a single rod of length \(l_{1}+l_{2}\). The coefficients of linear expansion for aluminium and steel are \(\alpha_{a}\) and \(\alpha_{s}\) respectively. If the length of each rod increase by the same amount when their temperature is raised by \(t^\circ C\), then find the ratio \(\dfrac{l_{1}}{\left(l_{1}+l_{2}\right)}\)

366749 A metallic tape gives correct value at \(25^\circ C\). A piece of wood is being meassured by this metallic tape at \(10^\circ C\). The reading is \(30\;cm\) on the tape, the real length of wooden piece must be

366750 Coefficient of linear expansion of brass and steel rods are \(\alpha_{1}\) and \(\alpha_{2}\). Lengths of brass and steel rods are \(\ell_{1}\) and \(\ell_{2}\) respectively. If \(\left(\ell_{2}-\ell_{1}\right)\) is maintained same at all temperatures, which one of the following relations holds good?

366746 The wooden wheel of radius \(R\) is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area \(S\) and length \(L . L\) is slightly less than \(2 \pi R\). To fit the ring on the wheel, it is heated so that its temperature rises by \(\Delta T\) and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is \(\alpha\) and its Young's modulus is \(Y\), the force that one part of the wheel applies on the other part is

366747 The variation of lengths of two metal rods \({A}\) and \({B}\) with change in temperature is shown in the figure. The ratio of \({\dfrac{\alpha_{A}}{\alpha_{B}}}\) is

366748 Two rods, one of aluminium and the other made of steel, having initial length \(l_{1}\) and \(l_{2}\) are connected together to form a single rod of length \(l_{1}+l_{2}\). The coefficients of linear expansion for aluminium and steel are \(\alpha_{a}\) and \(\alpha_{s}\) respectively. If the length of each rod increase by the same amount when their temperature is raised by \(t^\circ C\), then find the ratio \(\dfrac{l_{1}}{\left(l_{1}+l_{2}\right)}\)

366749 A metallic tape gives correct value at \(25^\circ C\). A piece of wood is being meassured by this metallic tape at \(10^\circ C\). The reading is \(30\;cm\) on the tape, the real length of wooden piece must be

366750 Coefficient of linear expansion of brass and steel rods are \(\alpha_{1}\) and \(\alpha_{2}\). Lengths of brass and steel rods are \(\ell_{1}\) and \(\ell_{2}\) respectively. If \(\left(\ell_{2}-\ell_{1}\right)\) is maintained same at all temperatures, which one of the following relations holds good?