366739 A circular disc made of iron is rotated about its axis at a constant velocity \(\omega\). Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from \(20^\circ C\) to \(50^\circ C\) keeping the angular velocity constant. (Coefficient of linear expansion of iron \(\left. { = 1.2 \times {{10}^{ - 5}}/^\circ C} \right)\).
366740
Three rods of equal length \(l\) are joined to form an equilateral triangle \(P Q R\). \(O\) is the mid point of \(P Q\). Distance \(O R\) remains same for small change in temperature. Coefficient of linear expansion for \(P R\) ad \(R Q\) is same, i.e., \(\alpha_{2}\) but that for \(P Q\) is \(\alpha_{1}\). Then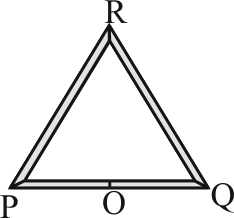
366739 A circular disc made of iron is rotated about its axis at a constant velocity \(\omega\). Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from \(20^\circ C\) to \(50^\circ C\) keeping the angular velocity constant. (Coefficient of linear expansion of iron \(\left. { = 1.2 \times {{10}^{ - 5}}/^\circ C} \right)\).
366740
Three rods of equal length \(l\) are joined to form an equilateral triangle \(P Q R\). \(O\) is the mid point of \(P Q\). Distance \(O R\) remains same for small change in temperature. Coefficient of linear expansion for \(P R\) ad \(R Q\) is same, i.e., \(\alpha_{2}\) but that for \(P Q\) is \(\alpha_{1}\). Then
366739 A circular disc made of iron is rotated about its axis at a constant velocity \(\omega\). Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from \(20^\circ C\) to \(50^\circ C\) keeping the angular velocity constant. (Coefficient of linear expansion of iron \(\left. { = 1.2 \times {{10}^{ - 5}}/^\circ C} \right)\).
366740
Three rods of equal length \(l\) are joined to form an equilateral triangle \(P Q R\). \(O\) is the mid point of \(P Q\). Distance \(O R\) remains same for small change in temperature. Coefficient of linear expansion for \(P R\) ad \(R Q\) is same, i.e., \(\alpha_{2}\) but that for \(P Q\) is \(\alpha_{1}\). Then
366739 A circular disc made of iron is rotated about its axis at a constant velocity \(\omega\). Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from \(20^\circ C\) to \(50^\circ C\) keeping the angular velocity constant. (Coefficient of linear expansion of iron \(\left. { = 1.2 \times {{10}^{ - 5}}/^\circ C} \right)\).
366740
Three rods of equal length \(l\) are joined to form an equilateral triangle \(P Q R\). \(O\) is the mid point of \(P Q\). Distance \(O R\) remains same for small change in temperature. Coefficient of linear expansion for \(P R\) ad \(R Q\) is same, i.e., \(\alpha_{2}\) but that for \(P Q\) is \(\alpha_{1}\). Then

