366652 A hot body placed in the air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being \(k\) times the temperature difference from the surrounding. Starting from \(t=0\), find the time at which the temperature difference between body and surrounding is equal to half of the initial temperature difference.
366654
A body cools in a surrounding which is at a constant temperature of \(\theta_{0}\). Assume that it obeys Newton's law of cooling. Its temperature \(\theta\) is plotted against time \(t\). Tangents are drawn to the curve at the points \(P\left(\theta=\theta_{1}\right)\) and \(Q\left(\theta=\theta_{2}\right)\). These tangents meet the time axis at angles of \(\phi_{2}\) and \(\phi_{1}\), as shown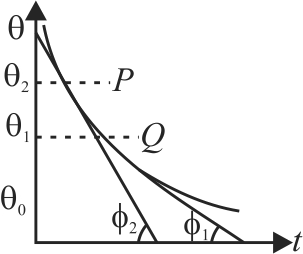
366655 Consider two hot bodies \(B_{1}\) and \(B_{2}\) which have temperatures \(100^\circ C\) and \(80^\circ C\) respectively at \(t = 0\). The temperature of the surroundings is \(40^\circ C\). The ratio of the respective rates of cooling and of these two bodies at \(t = 0\) will be
366652 A hot body placed in the air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being \(k\) times the temperature difference from the surrounding. Starting from \(t=0\), find the time at which the temperature difference between body and surrounding is equal to half of the initial temperature difference.
366654
A body cools in a surrounding which is at a constant temperature of \(\theta_{0}\). Assume that it obeys Newton's law of cooling. Its temperature \(\theta\) is plotted against time \(t\). Tangents are drawn to the curve at the points \(P\left(\theta=\theta_{1}\right)\) and \(Q\left(\theta=\theta_{2}\right)\). These tangents meet the time axis at angles of \(\phi_{2}\) and \(\phi_{1}\), as shown
366655 Consider two hot bodies \(B_{1}\) and \(B_{2}\) which have temperatures \(100^\circ C\) and \(80^\circ C\) respectively at \(t = 0\). The temperature of the surroundings is \(40^\circ C\). The ratio of the respective rates of cooling and of these two bodies at \(t = 0\) will be
366652 A hot body placed in the air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being \(k\) times the temperature difference from the surrounding. Starting from \(t=0\), find the time at which the temperature difference between body and surrounding is equal to half of the initial temperature difference.
366654
A body cools in a surrounding which is at a constant temperature of \(\theta_{0}\). Assume that it obeys Newton's law of cooling. Its temperature \(\theta\) is plotted against time \(t\). Tangents are drawn to the curve at the points \(P\left(\theta=\theta_{1}\right)\) and \(Q\left(\theta=\theta_{2}\right)\). These tangents meet the time axis at angles of \(\phi_{2}\) and \(\phi_{1}\), as shown
366655 Consider two hot bodies \(B_{1}\) and \(B_{2}\) which have temperatures \(100^\circ C\) and \(80^\circ C\) respectively at \(t = 0\). The temperature of the surroundings is \(40^\circ C\). The ratio of the respective rates of cooling and of these two bodies at \(t = 0\) will be
366652 A hot body placed in the air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being \(k\) times the temperature difference from the surrounding. Starting from \(t=0\), find the time at which the temperature difference between body and surrounding is equal to half of the initial temperature difference.
366654
A body cools in a surrounding which is at a constant temperature of \(\theta_{0}\). Assume that it obeys Newton's law of cooling. Its temperature \(\theta\) is plotted against time \(t\). Tangents are drawn to the curve at the points \(P\left(\theta=\theta_{1}\right)\) and \(Q\left(\theta=\theta_{2}\right)\). These tangents meet the time axis at angles of \(\phi_{2}\) and \(\phi_{1}\), as shown
366655 Consider two hot bodies \(B_{1}\) and \(B_{2}\) which have temperatures \(100^\circ C\) and \(80^\circ C\) respectively at \(t = 0\). The temperature of the surroundings is \(40^\circ C\). The ratio of the respective rates of cooling and of these two bodies at \(t = 0\) will be
366652 A hot body placed in the air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being \(k\) times the temperature difference from the surrounding. Starting from \(t=0\), find the time at which the temperature difference between body and surrounding is equal to half of the initial temperature difference.
366654
A body cools in a surrounding which is at a constant temperature of \(\theta_{0}\). Assume that it obeys Newton's law of cooling. Its temperature \(\theta\) is plotted against time \(t\). Tangents are drawn to the curve at the points \(P\left(\theta=\theta_{1}\right)\) and \(Q\left(\theta=\theta_{2}\right)\). These tangents meet the time axis at angles of \(\phi_{2}\) and \(\phi_{1}\), as shown
366655 Consider two hot bodies \(B_{1}\) and \(B_{2}\) which have temperatures \(100^\circ C\) and \(80^\circ C\) respectively at \(t = 0\). The temperature of the surroundings is \(40^\circ C\). The ratio of the respective rates of cooling and of these two bodies at \(t = 0\) will be