366403
Two rectangular blocks, having identical dimensions, can be arranged either in configuration \(I\) or in configuration II as shown in the figure, one of the blocks has thermal conductivity \(K\) and the other \(2K\). The temperature difference between the two ends along the \(x\) axis is the same in both the configurations. It takes 9 min to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is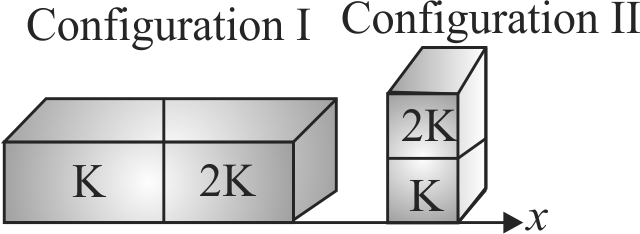
366404
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\) respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state is
\(\left(\dfrac{A\left(T_{2}-T_{1}\right) K}{x}\right) f\), with \(f\) equal to: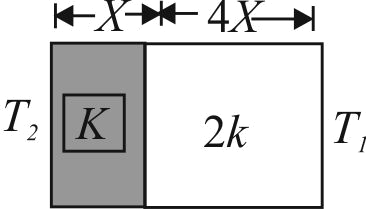
366405
The temperature of the two outer surface of a composite slab, consisting of two meterials having coefficient of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\), respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state \(i\) \(s\left( {\frac{{A\left( {{T_2} - {T_1}} \right)K}}{x}} \right)f\), the value of \(f\) is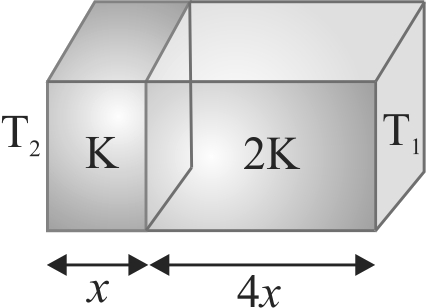
366403
Two rectangular blocks, having identical dimensions, can be arranged either in configuration \(I\) or in configuration II as shown in the figure, one of the blocks has thermal conductivity \(K\) and the other \(2K\). The temperature difference between the two ends along the \(x\) axis is the same in both the configurations. It takes 9 min to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is
366404
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\) respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state is
\(\left(\dfrac{A\left(T_{2}-T_{1}\right) K}{x}\right) f\), with \(f\) equal to:
366405
The temperature of the two outer surface of a composite slab, consisting of two meterials having coefficient of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\), respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state \(i\) \(s\left( {\frac{{A\left( {{T_2} - {T_1}} \right)K}}{x}} \right)f\), the value of \(f\) is
366403
Two rectangular blocks, having identical dimensions, can be arranged either in configuration \(I\) or in configuration II as shown in the figure, one of the blocks has thermal conductivity \(K\) and the other \(2K\). The temperature difference between the two ends along the \(x\) axis is the same in both the configurations. It takes 9 min to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is
366404
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\) respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state is
\(\left(\dfrac{A\left(T_{2}-T_{1}\right) K}{x}\right) f\), with \(f\) equal to:
366405
The temperature of the two outer surface of a composite slab, consisting of two meterials having coefficient of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\), respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state \(i\) \(s\left( {\frac{{A\left( {{T_2} - {T_1}} \right)K}}{x}} \right)f\), the value of \(f\) is
366403
Two rectangular blocks, having identical dimensions, can be arranged either in configuration \(I\) or in configuration II as shown in the figure, one of the blocks has thermal conductivity \(K\) and the other \(2K\). The temperature difference between the two ends along the \(x\) axis is the same in both the configurations. It takes 9 min to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is
366404
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\) respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state is
\(\left(\dfrac{A\left(T_{2}-T_{1}\right) K}{x}\right) f\), with \(f\) equal to:
366405
The temperature of the two outer surface of a composite slab, consisting of two meterials having coefficient of thermal conductivity \(K\) and \(2 K\) and thickness \(x\) and \(4 x\), respectively are \(T_{2}\) and \(T_{1}\left(T_{2}>T_{1}\right)\). The rate of heat transfer through the slab, in a steady state \(i\) \(s\left( {\frac{{A\left( {{T_2} - {T_1}} \right)K}}{x}} \right)f\), the value of \(f\) is
