366393
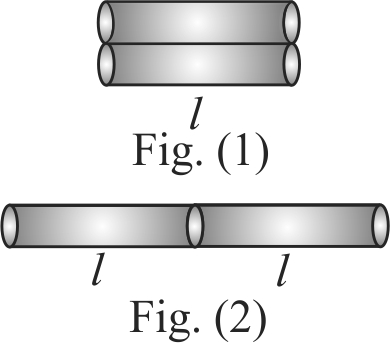
A composite rod made of three rods of equal length and cross section, as shown in figure. The thermal conductivities of materiales of rods are \({k / 2,5 k}\) and \({k}\), respectively. The end \({A}\) and end \({B}\) are at constant temperture. The effective thermal conductivity of the bar is \({\left(T_{1}>T_{2}\right)}\)
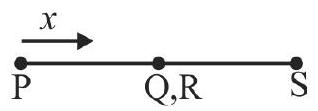
366395 The ends \(Q\) and \(R\) of two thin wires, \(P Q\) and \(RS\), are joined together. Initially each of the wires has a length of \(1m\) at \(10^\circ C\). Now the end \(P\) is maintained at \(10^\circ C\), while the end \(S\) is heated and maintained at \(400^\circ C\). The system is thermally insulted from its surroundings. If the thermal conductivity of wire \(PQ\) is twice that of the wire RS and the coefficient of linear thermal expansion of \(PQ\) is \(1.2 \times {10^{ - 5}}\;{K^{ - 1}}\), the change in length of the wire \(P Q\) is
366396
A cylinder \(A\) of a material of thermal conductivity \(K_{1}\) is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity \(K_{2}\). The two ends of the combined system are maintained at two different temperatures. If the effective thermal conductivity of the system is \(\dfrac{4 K_{1}+5 K_{2}}{9}\), find the ratio of outer radius of the shell to the radius of the cylinder.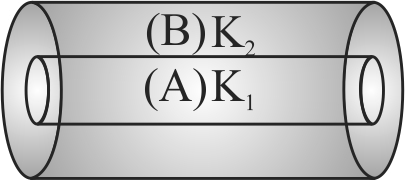
366393
A composite rod made of three rods of equal length and cross section, as shown in figure. The thermal conductivities of materiales of rods are \({k / 2,5 k}\) and \({k}\), respectively. The end \({A}\) and end \({B}\) are at constant temperture. The effective thermal conductivity of the bar is \({\left(T_{1}>T_{2}\right)}\)
366395 The ends \(Q\) and \(R\) of two thin wires, \(P Q\) and \(RS\), are joined together. Initially each of the wires has a length of \(1m\) at \(10^\circ C\). Now the end \(P\) is maintained at \(10^\circ C\), while the end \(S\) is heated and maintained at \(400^\circ C\). The system is thermally insulted from its surroundings. If the thermal conductivity of wire \(PQ\) is twice that of the wire RS and the coefficient of linear thermal expansion of \(PQ\) is \(1.2 \times {10^{ - 5}}\;{K^{ - 1}}\), the change in length of the wire \(P Q\) is
366396
A cylinder \(A\) of a material of thermal conductivity \(K_{1}\) is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity \(K_{2}\). The two ends of the combined system are maintained at two different temperatures. If the effective thermal conductivity of the system is \(\dfrac{4 K_{1}+5 K_{2}}{9}\), find the ratio of outer radius of the shell to the radius of the cylinder.
366393
A composite rod made of three rods of equal length and cross section, as shown in figure. The thermal conductivities of materiales of rods are \({k / 2,5 k}\) and \({k}\), respectively. The end \({A}\) and end \({B}\) are at constant temperture. The effective thermal conductivity of the bar is \({\left(T_{1}>T_{2}\right)}\)
366395 The ends \(Q\) and \(R\) of two thin wires, \(P Q\) and \(RS\), are joined together. Initially each of the wires has a length of \(1m\) at \(10^\circ C\). Now the end \(P\) is maintained at \(10^\circ C\), while the end \(S\) is heated and maintained at \(400^\circ C\). The system is thermally insulted from its surroundings. If the thermal conductivity of wire \(PQ\) is twice that of the wire RS and the coefficient of linear thermal expansion of \(PQ\) is \(1.2 \times {10^{ - 5}}\;{K^{ - 1}}\), the change in length of the wire \(P Q\) is
366396
A cylinder \(A\) of a material of thermal conductivity \(K_{1}\) is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity \(K_{2}\). The two ends of the combined system are maintained at two different temperatures. If the effective thermal conductivity of the system is \(\dfrac{4 K_{1}+5 K_{2}}{9}\), find the ratio of outer radius of the shell to the radius of the cylinder.
366393
A composite rod made of three rods of equal length and cross section, as shown in figure. The thermal conductivities of materiales of rods are \({k / 2,5 k}\) and \({k}\), respectively. The end \({A}\) and end \({B}\) are at constant temperture. The effective thermal conductivity of the bar is \({\left(T_{1}>T_{2}\right)}\)
366395 The ends \(Q\) and \(R\) of two thin wires, \(P Q\) and \(RS\), are joined together. Initially each of the wires has a length of \(1m\) at \(10^\circ C\). Now the end \(P\) is maintained at \(10^\circ C\), while the end \(S\) is heated and maintained at \(400^\circ C\). The system is thermally insulted from its surroundings. If the thermal conductivity of wire \(PQ\) is twice that of the wire RS and the coefficient of linear thermal expansion of \(PQ\) is \(1.2 \times {10^{ - 5}}\;{K^{ - 1}}\), the change in length of the wire \(P Q\) is
366396
A cylinder \(A\) of a material of thermal conductivity \(K_{1}\) is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity \(K_{2}\). The two ends of the combined system are maintained at two different temperatures. If the effective thermal conductivity of the system is \(\dfrac{4 K_{1}+5 K_{2}}{9}\), find the ratio of outer radius of the shell to the radius of the cylinder.
366393
A composite rod made of three rods of equal length and cross section, as shown in figure. The thermal conductivities of materiales of rods are \({k / 2,5 k}\) and \({k}\), respectively. The end \({A}\) and end \({B}\) are at constant temperture. The effective thermal conductivity of the bar is \({\left(T_{1}>T_{2}\right)}\)
366395 The ends \(Q\) and \(R\) of two thin wires, \(P Q\) and \(RS\), are joined together. Initially each of the wires has a length of \(1m\) at \(10^\circ C\). Now the end \(P\) is maintained at \(10^\circ C\), while the end \(S\) is heated and maintained at \(400^\circ C\). The system is thermally insulted from its surroundings. If the thermal conductivity of wire \(PQ\) is twice that of the wire RS and the coefficient of linear thermal expansion of \(PQ\) is \(1.2 \times {10^{ - 5}}\;{K^{ - 1}}\), the change in length of the wire \(P Q\) is
366396
A cylinder \(A\) of a material of thermal conductivity \(K_{1}\) is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity \(K_{2}\). The two ends of the combined system are maintained at two different temperatures. If the effective thermal conductivity of the system is \(\dfrac{4 K_{1}+5 K_{2}}{9}\), find the ratio of outer radius of the shell to the radius of the cylinder.