363388
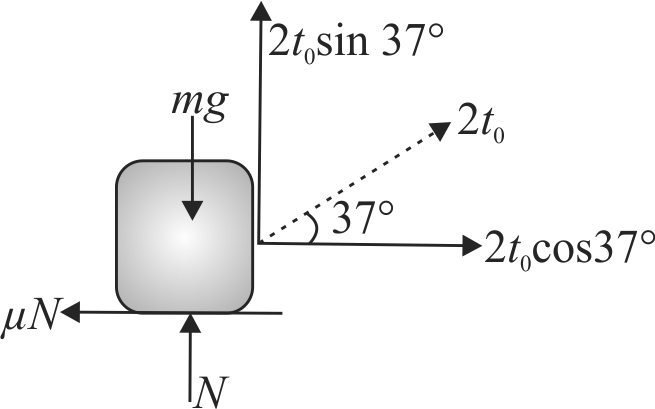
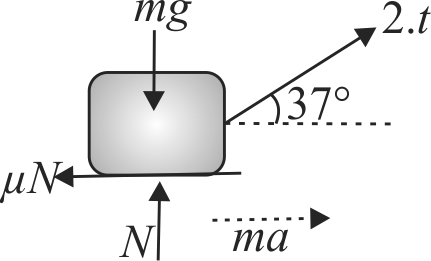
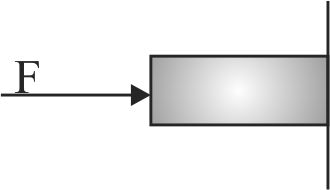
A block of masss \(m=3 {~kg}\) is resting over a rough horizontal surface having coefficient of friction \(\mu=1 / 3\). The block is pulled to the right by applying a force \(F\), inclined at angle \(37^{\circ}\) with the horizontal as shown in figure. The force increases with time according to law \(F=2 t\) newton.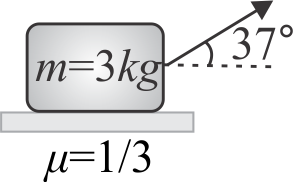
If the velocity of the block at \(t = 10\,\,\sec \) is found to be \(\dfrac{25}{N} {~ms}^{2}\). Find the value of '\(N\)'. \(\left(g=10 {~ms}^{-2}\right)\)
363388
A block of masss \(m=3 {~kg}\) is resting over a rough horizontal surface having coefficient of friction \(\mu=1 / 3\). The block is pulled to the right by applying a force \(F\), inclined at angle \(37^{\circ}\) with the horizontal as shown in figure. The force increases with time according to law \(F=2 t\) newton.
If the velocity of the block at \(t = 10\,\,\sec \) is found to be \(\dfrac{25}{N} {~ms}^{2}\). Find the value of '\(N\)'. \(\left(g=10 {~ms}^{-2}\right)\)
363388
A block of masss \(m=3 {~kg}\) is resting over a rough horizontal surface having coefficient of friction \(\mu=1 / 3\). The block is pulled to the right by applying a force \(F\), inclined at angle \(37^{\circ}\) with the horizontal as shown in figure. The force increases with time according to law \(F=2 t\) newton.
If the velocity of the block at \(t = 10\,\,\sec \) is found to be \(\dfrac{25}{N} {~ms}^{2}\). Find the value of '\(N\)'. \(\left(g=10 {~ms}^{-2}\right)\)
363388
A block of masss \(m=3 {~kg}\) is resting over a rough horizontal surface having coefficient of friction \(\mu=1 / 3\). The block is pulled to the right by applying a force \(F\), inclined at angle \(37^{\circ}\) with the horizontal as shown in figure. The force increases with time according to law \(F=2 t\) newton.
If the velocity of the block at \(t = 10\,\,\sec \) is found to be \(\dfrac{25}{N} {~ms}^{2}\). Find the value of '\(N\)'. \(\left(g=10 {~ms}^{-2}\right)\)