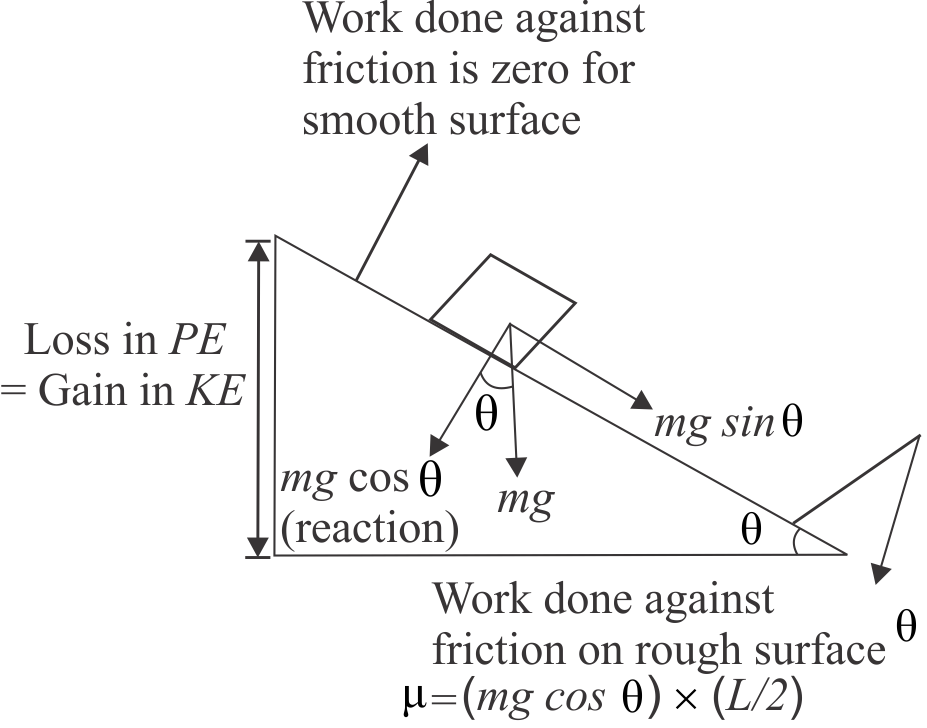
363356 The upper half of an inclined plane of inclination \(\theta\) is perfectly smooth while the lower half rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by
363358
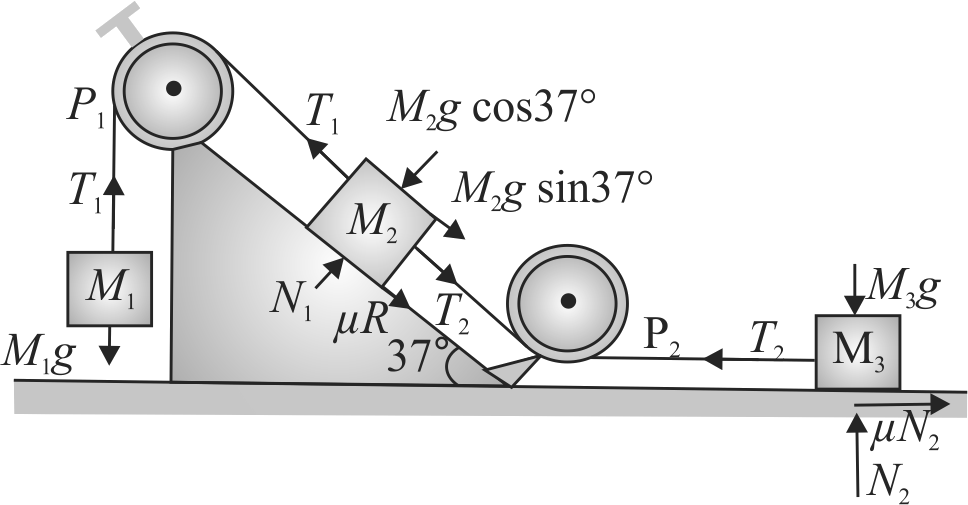
Masses \(M_{1}, M_{2}\) and \(M_{3}\) are connected by light strings which pass over pulleys \(P_{1}\) and \(P_{2}\) as shown. The masses move such that the string between \(P_{1}\) and \(P_{2}\) is parallel to incline and the string between \(P_{2}\) and \(M_{2}\) is horizontal, \(M_{2}=M_{3}=4 {~kg}\). The coefficient of kinetic friction between masses and the surface is 0.25 . The angle of inclination of plane is \(37^{\circ}\) to the horizontal. If the mass \(M_{1}\) moves downward with uniform velocity, find the tension in the horizontal string. (Given \(g=10 {~m} / {s}^{2}\) )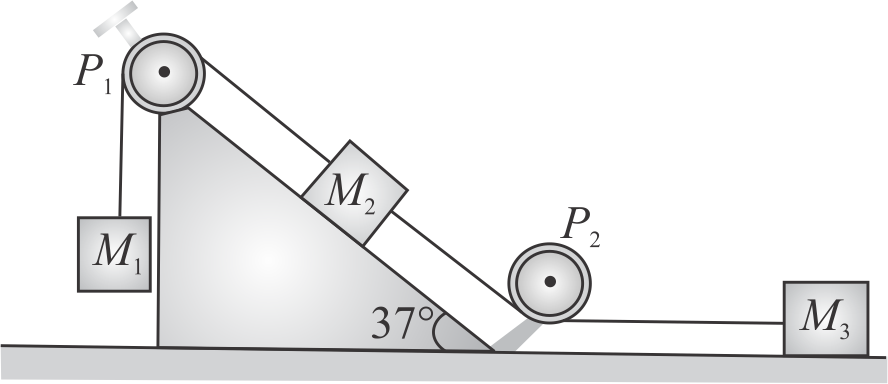
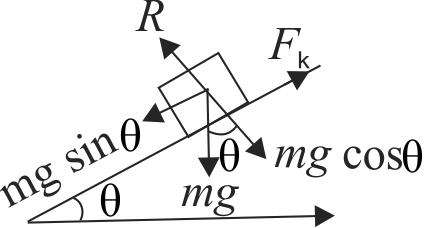
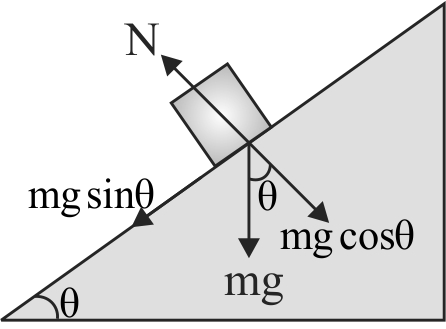
363359 The upper half of an inclined plane of inclination \(\theta \) is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
363356 The upper half of an inclined plane of inclination \(\theta\) is perfectly smooth while the lower half rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by
363358
Masses \(M_{1}, M_{2}\) and \(M_{3}\) are connected by light strings which pass over pulleys \(P_{1}\) and \(P_{2}\) as shown. The masses move such that the string between \(P_{1}\) and \(P_{2}\) is parallel to incline and the string between \(P_{2}\) and \(M_{2}\) is horizontal, \(M_{2}=M_{3}=4 {~kg}\). The coefficient of kinetic friction between masses and the surface is 0.25 . The angle of inclination of plane is \(37^{\circ}\) to the horizontal. If the mass \(M_{1}\) moves downward with uniform velocity, find the tension in the horizontal string. (Given \(g=10 {~m} / {s}^{2}\) )
363359 The upper half of an inclined plane of inclination \(\theta \) is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
363356 The upper half of an inclined plane of inclination \(\theta\) is perfectly smooth while the lower half rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by
363358
Masses \(M_{1}, M_{2}\) and \(M_{3}\) are connected by light strings which pass over pulleys \(P_{1}\) and \(P_{2}\) as shown. The masses move such that the string between \(P_{1}\) and \(P_{2}\) is parallel to incline and the string between \(P_{2}\) and \(M_{2}\) is horizontal, \(M_{2}=M_{3}=4 {~kg}\). The coefficient of kinetic friction between masses and the surface is 0.25 . The angle of inclination of plane is \(37^{\circ}\) to the horizontal. If the mass \(M_{1}\) moves downward with uniform velocity, find the tension in the horizontal string. (Given \(g=10 {~m} / {s}^{2}\) )
363359 The upper half of an inclined plane of inclination \(\theta \) is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
363356 The upper half of an inclined plane of inclination \(\theta\) is perfectly smooth while the lower half rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by
363358
Masses \(M_{1}, M_{2}\) and \(M_{3}\) are connected by light strings which pass over pulleys \(P_{1}\) and \(P_{2}\) as shown. The masses move such that the string between \(P_{1}\) and \(P_{2}\) is parallel to incline and the string between \(P_{2}\) and \(M_{2}\) is horizontal, \(M_{2}=M_{3}=4 {~kg}\). The coefficient of kinetic friction between masses and the surface is 0.25 . The angle of inclination of plane is \(37^{\circ}\) to the horizontal. If the mass \(M_{1}\) moves downward with uniform velocity, find the tension in the horizontal string. (Given \(g=10 {~m} / {s}^{2}\) )
363359 The upper half of an inclined plane of inclination \(\theta \) is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by