363354
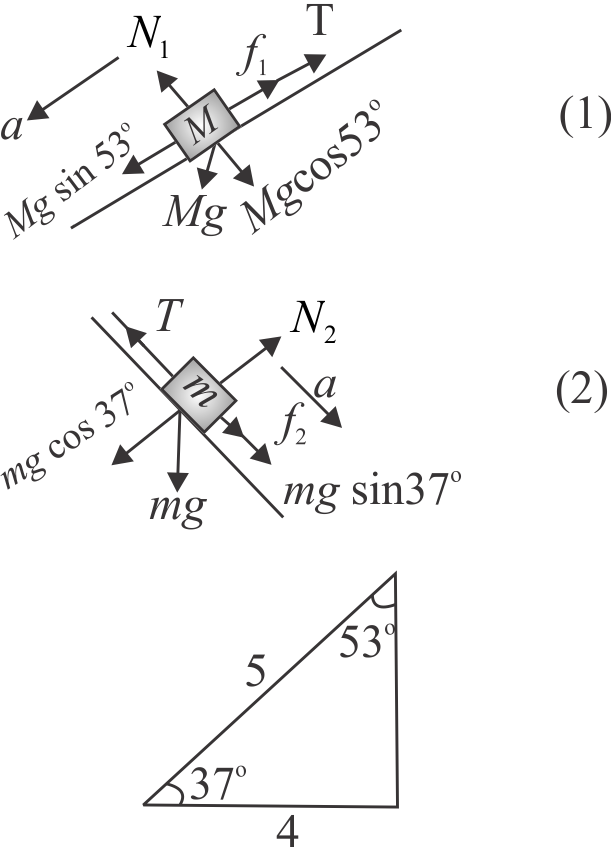
In the given arrangement of a doubly inclined plane two blocks of masses \(M\) and \(m\) are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is 0.25 . The value of \(m\) , for which \(M = 10\,kg\) will move down with an acceleration of \(2\;m/{s^2}\) is (Take \(g = 10\;m/{s^2}{\rm{ }}\) and \(\tan \,\,37^\circ = \frac{3}{4}\) )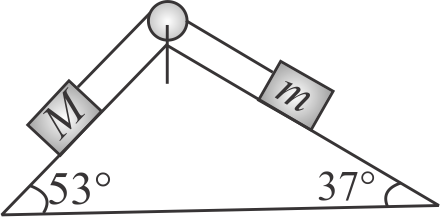
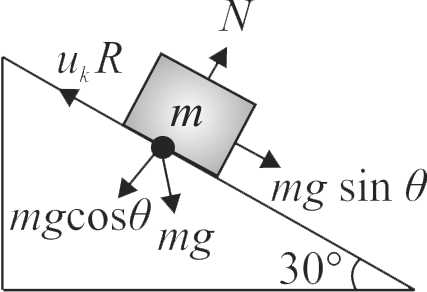
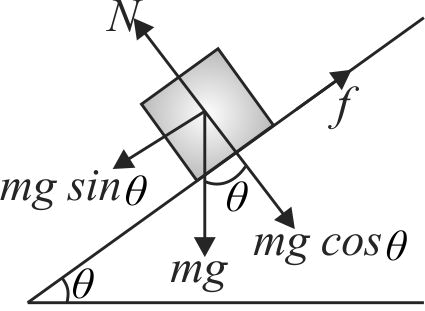
363355 A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches \(30^\circ \) the box starts to slip and slides 4.0 \(m\) down the plank in 4.0 \(s\). The coefficients of static and kinetic friction between the box and the plank will be, respectively :
363354
In the given arrangement of a doubly inclined plane two blocks of masses \(M\) and \(m\) are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is 0.25 . The value of \(m\) , for which \(M = 10\,kg\) will move down with an acceleration of \(2\;m/{s^2}\) is (Take \(g = 10\;m/{s^2}{\rm{ }}\) and \(\tan \,\,37^\circ = \frac{3}{4}\) )
363355 A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches \(30^\circ \) the box starts to slip and slides 4.0 \(m\) down the plank in 4.0 \(s\). The coefficients of static and kinetic friction between the box and the plank will be, respectively :
363354
In the given arrangement of a doubly inclined plane two blocks of masses \(M\) and \(m\) are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is 0.25 . The value of \(m\) , for which \(M = 10\,kg\) will move down with an acceleration of \(2\;m/{s^2}\) is (Take \(g = 10\;m/{s^2}{\rm{ }}\) and \(\tan \,\,37^\circ = \frac{3}{4}\) )
363355 A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches \(30^\circ \) the box starts to slip and slides 4.0 \(m\) down the plank in 4.0 \(s\). The coefficients of static and kinetic friction between the box and the plank will be, respectively :
363354
In the given arrangement of a doubly inclined plane two blocks of masses \(M\) and \(m\) are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is 0.25 . The value of \(m\) , for which \(M = 10\,kg\) will move down with an acceleration of \(2\;m/{s^2}\) is (Take \(g = 10\;m/{s^2}{\rm{ }}\) and \(\tan \,\,37^\circ = \frac{3}{4}\) )
363355 A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches \(30^\circ \) the box starts to slip and slides 4.0 \(m\) down the plank in 4.0 \(s\). The coefficients of static and kinetic friction between the box and the plank will be, respectively :