Explanation:
Let \(T\) be the tension in the string \(C\). Then in equilibrium,
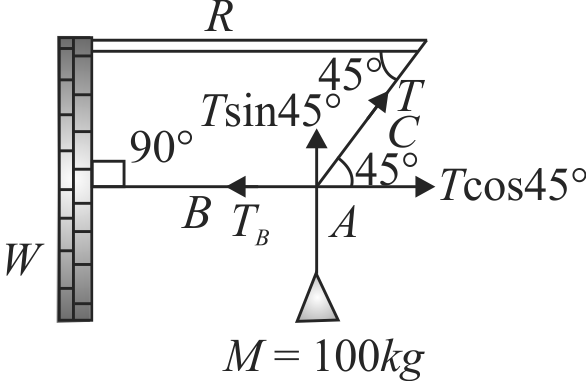
\(T\sin 45^\circ = Mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(T\cos 45^\circ = {T_B}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mkern 1mu} \left( 2 \right)\)
Divide (1) by (2) \(\therefore = \frac{{T\,\sin 45^\circ }}{{T\,\cos 45^\circ }} = \frac{{Mg}}{{{T_B}}}\)
\( \Rightarrow {T_B} = 100\,g\,N\)