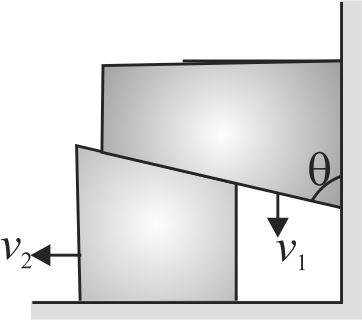
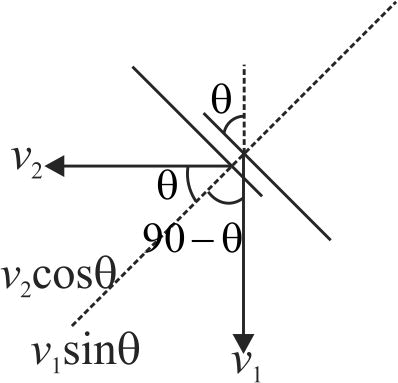
363266
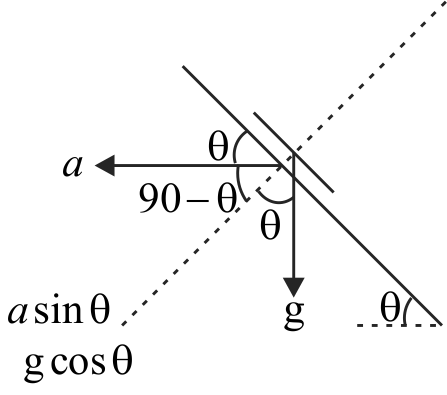
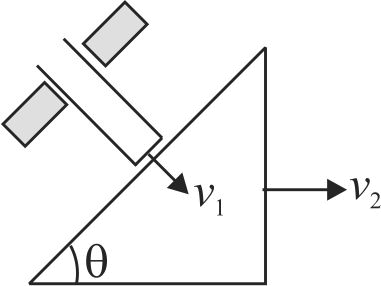
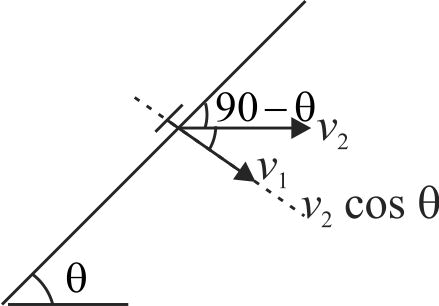
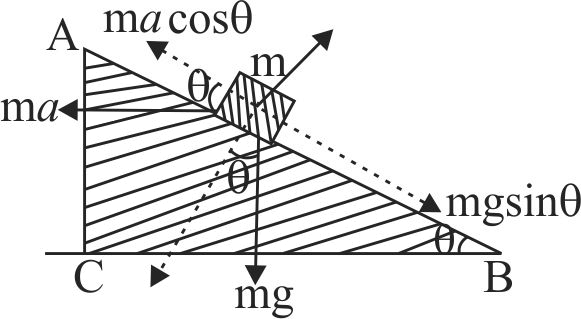
A block of mass \(m\) is placed on a smooth inclined wedge \(ABC\) of inclination \(\theta \) as shown in the figure. The wedge is given an acceleration ‘\(a\)’ towards the right. The relation between \(a\) and \(\theta \) for the block to remain stationary on the wedge is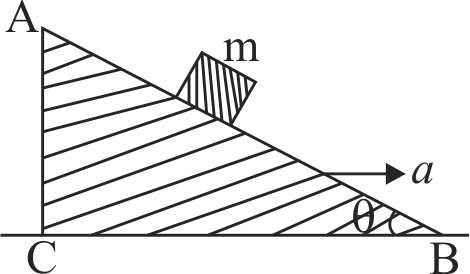
363266
A block of mass \(m\) is placed on a smooth inclined wedge \(ABC\) of inclination \(\theta \) as shown in the figure. The wedge is given an acceleration ‘\(a\)’ towards the right. The relation between \(a\) and \(\theta \) for the block to remain stationary on the wedge is
363266
A block of mass \(m\) is placed on a smooth inclined wedge \(ABC\) of inclination \(\theta \) as shown in the figure. The wedge is given an acceleration ‘\(a\)’ towards the right. The relation between \(a\) and \(\theta \) for the block to remain stationary on the wedge is
363266
A block of mass \(m\) is placed on a smooth inclined wedge \(ABC\) of inclination \(\theta \) as shown in the figure. The wedge is given an acceleration ‘\(a\)’ towards the right. The relation between \(a\) and \(\theta \) for the block to remain stationary on the wedge is