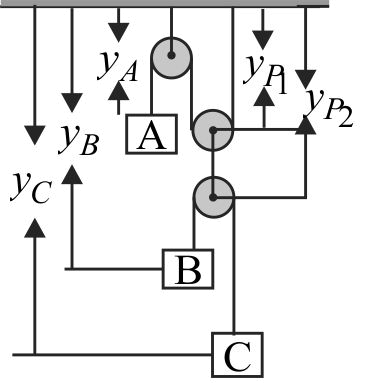
Explanation:
Express the position of moveable pulleys and blocks with respect to fixed frame as shown in the figure
String – 1:
\({l_1} = {y_A} + {y_{{P_1}}} + {y_{{p_1}}} + c = {y_A} + 2{y_{{P_1}}} + c\)
\(0 = {V_A} + 2{V_{{p_1}}}\)
\( \Rightarrow 0 = {a_A} + 2{a_{{p_1}}}\,\,\,\, \to \,\,\,\,\left( 1 \right)\)
String – 2:
\({l_2} = ({y_B} - {y_{{p_2}}}) + ({y_C} - {y_{{p_2}}})\)
\({l_2} = {y_B} - 2{y_{{p_2}}} + {y_C}\)
\(0 = {V_B} - 2{V_{{p_2}}} + {V_C}\)
\(0 = {a_B} - 2{a_{{p_2}}} + {a_C}\;\;\;\; \to (2)\)
From the diagram \({a_{{p_1}}} = {a_{{p_2}}}\)
Since two pulleys are connected by a vertical string
From (1) and (2) we get
\({a_B} + {a_C} + {a_A} = 0\)
We assume an arbitrary sign convention.Take downward direction as \(( + )ve\)
Given \({a_A} = 5\,m/{s^2}\), \({a_B} = - 4m/{s^2}\)
\( \Rightarrow {a_C} = - 1\,m/{s^2}\) i.e., block \(C\) goes upward with \(1\,m/{s^2}\)