Explanation:
For \({m_{2}}\),
\(T - {m_2}g = {m_2}(2a)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Free body diagram \((FBD)\) of \({m_{2}}\)

For \({m_1}{m_1}g - 2{m_2} = {m_1}(a)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Free body diagram \((FBD)\) of \({m_{1}}\)
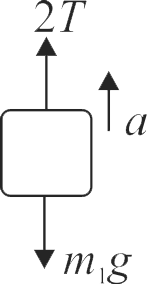
From Eqs. (1) and (2), we get
\(\begin{aligned}& m_{1} g-2 m_{2} g=4 m_{2} a+m_{1} a \\\Rightarrow & a=0 {~m} / {s}^{2} \\\text { Or } & T=m_{2} g=10 {~N}\end{aligned}\)
For \({m, 2 T=m g \Rightarrow m=\dfrac{20}{10}=2 {~kg}}\)
Free body diagram of \({m}\)
\(\begin{aligned}& m g=2 T \\\Rightarrow \quad & m=\dfrac{2 \times 10}{10}=2 {~kg}\end{aligned}\)
