363245
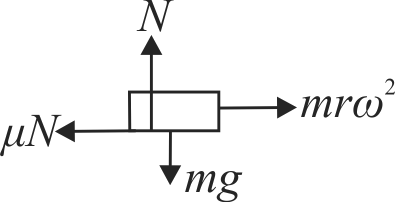
\(A \operatorname{rod} A B\) of length 2 \(m\) is hinged at point \(A\) and its other end \(B\) is attached to a platform on which a block of mass \(m\) is kept. Rod rotates about point \(A\) maintaining angle \(\theta=30^{\circ}\) with the vertical in such a way that platform remains horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is \(\mu=0.1\), then find the maximum angular velocity of rod so that the block does not slip on the platform. \(\left(g=10 {~m} {~s}^{-2}\right)\)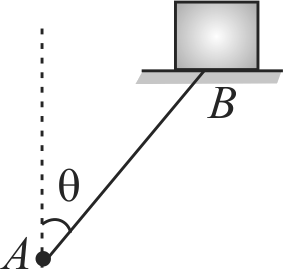
363245
\(A \operatorname{rod} A B\) of length 2 \(m\) is hinged at point \(A\) and its other end \(B\) is attached to a platform on which a block of mass \(m\) is kept. Rod rotates about point \(A\) maintaining angle \(\theta=30^{\circ}\) with the vertical in such a way that platform remains horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is \(\mu=0.1\), then find the maximum angular velocity of rod so that the block does not slip on the platform. \(\left(g=10 {~m} {~s}^{-2}\right)\)