363104
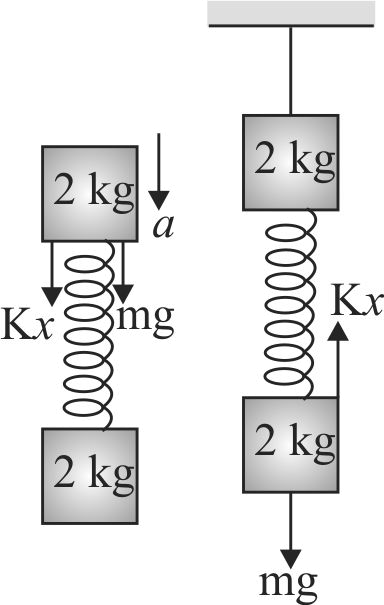
Two blocks of mass 2 \(kg\) are connected by a massless ideal spring of spring constant \(K = 10\,{\rm{N/m}}{\rm{.}}\) The upper block is suspended from roof by a light string \(A\). The system shown is in equilibrium. The string \(A\) is now cut, the acceleration of upper block just after the string \(A\) is cut will be \((g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}})\)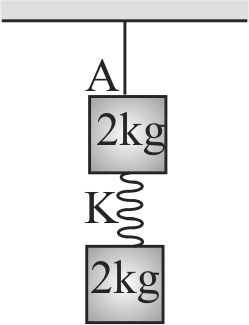
363106
A block of weight \({W}\) produces an extension of \(9\,cm\) when it is hung by an elastic spring of length \(60\,cm\) and is in equilibrium. The spring is cut into two parts, one of length \(40\,cm\) and the other of length \(20\,cm\). The same load \({W}\) hangs in equilibrium supported by both parts as shown in the figure. Find the extension in the spring.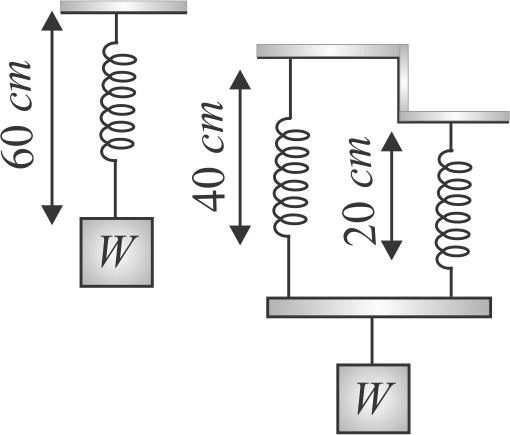
363107
Three blocks of masses \(2\;kg,3\;kg\) and \(5\;kg\) are connected to each other with light string and are then placed on a smooth frictionless surface. The system is pulled with force \(F\) from side of the lighter mass so that it moves with an acceleration of \(1\;m{s^{ - 2}},{T_1}\) and \(T_{2}\) denote the tension in the other strings. The value of \(F\) is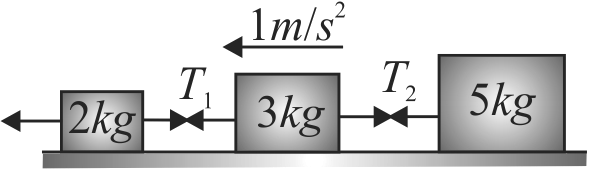
363104
Two blocks of mass 2 \(kg\) are connected by a massless ideal spring of spring constant \(K = 10\,{\rm{N/m}}{\rm{.}}\) The upper block is suspended from roof by a light string \(A\). The system shown is in equilibrium. The string \(A\) is now cut, the acceleration of upper block just after the string \(A\) is cut will be \((g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}})\)
363106
A block of weight \({W}\) produces an extension of \(9\,cm\) when it is hung by an elastic spring of length \(60\,cm\) and is in equilibrium. The spring is cut into two parts, one of length \(40\,cm\) and the other of length \(20\,cm\). The same load \({W}\) hangs in equilibrium supported by both parts as shown in the figure. Find the extension in the spring.
363107
Three blocks of masses \(2\;kg,3\;kg\) and \(5\;kg\) are connected to each other with light string and are then placed on a smooth frictionless surface. The system is pulled with force \(F\) from side of the lighter mass so that it moves with an acceleration of \(1\;m{s^{ - 2}},{T_1}\) and \(T_{2}\) denote the tension in the other strings. The value of \(F\) is
363104
Two blocks of mass 2 \(kg\) are connected by a massless ideal spring of spring constant \(K = 10\,{\rm{N/m}}{\rm{.}}\) The upper block is suspended from roof by a light string \(A\). The system shown is in equilibrium. The string \(A\) is now cut, the acceleration of upper block just after the string \(A\) is cut will be \((g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}})\)
363106
A block of weight \({W}\) produces an extension of \(9\,cm\) when it is hung by an elastic spring of length \(60\,cm\) and is in equilibrium. The spring is cut into two parts, one of length \(40\,cm\) and the other of length \(20\,cm\). The same load \({W}\) hangs in equilibrium supported by both parts as shown in the figure. Find the extension in the spring.
363107
Three blocks of masses \(2\;kg,3\;kg\) and \(5\;kg\) are connected to each other with light string and are then placed on a smooth frictionless surface. The system is pulled with force \(F\) from side of the lighter mass so that it moves with an acceleration of \(1\;m{s^{ - 2}},{T_1}\) and \(T_{2}\) denote the tension in the other strings. The value of \(F\) is
363104
Two blocks of mass 2 \(kg\) are connected by a massless ideal spring of spring constant \(K = 10\,{\rm{N/m}}{\rm{.}}\) The upper block is suspended from roof by a light string \(A\). The system shown is in equilibrium. The string \(A\) is now cut, the acceleration of upper block just after the string \(A\) is cut will be \((g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}})\)
363106
A block of weight \({W}\) produces an extension of \(9\,cm\) when it is hung by an elastic spring of length \(60\,cm\) and is in equilibrium. The spring is cut into two parts, one of length \(40\,cm\) and the other of length \(20\,cm\). The same load \({W}\) hangs in equilibrium supported by both parts as shown in the figure. Find the extension in the spring.
363107
Three blocks of masses \(2\;kg,3\;kg\) and \(5\;kg\) are connected to each other with light string and are then placed on a smooth frictionless surface. The system is pulled with force \(F\) from side of the lighter mass so that it moves with an acceleration of \(1\;m{s^{ - 2}},{T_1}\) and \(T_{2}\) denote the tension in the other strings. The value of \(F\) is