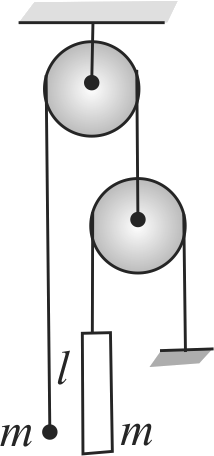
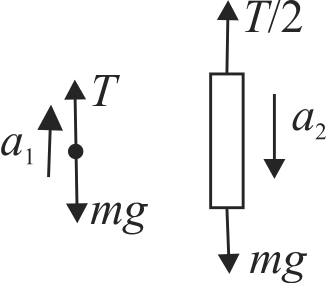
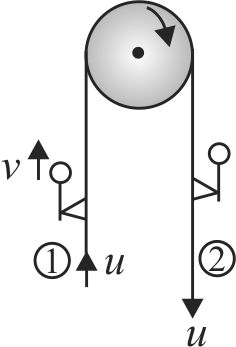
363069 A massless string of length \(l\) passes over a frictionless pulley with horizontal axis. Two monkeys hang from the ends of the string at the distance \(l\)/2 from the pulley, a monkey start climbing up with a speed \(v\) relative to the string and the second with speed of 2 \(v\). Both monkeys have got same masses. The time taken by the first and second monkeys in reaching the pulleys are respectively.
363069 A massless string of length \(l\) passes over a frictionless pulley with horizontal axis. Two monkeys hang from the ends of the string at the distance \(l\)/2 from the pulley, a monkey start climbing up with a speed \(v\) relative to the string and the second with speed of 2 \(v\). Both monkeys have got same masses. The time taken by the first and second monkeys in reaching the pulleys are respectively.
363069 A massless string of length \(l\) passes over a frictionless pulley with horizontal axis. Two monkeys hang from the ends of the string at the distance \(l\)/2 from the pulley, a monkey start climbing up with a speed \(v\) relative to the string and the second with speed of 2 \(v\). Both monkeys have got same masses. The time taken by the first and second monkeys in reaching the pulleys are respectively.
363069 A massless string of length \(l\) passes over a frictionless pulley with horizontal axis. Two monkeys hang from the ends of the string at the distance \(l\)/2 from the pulley, a monkey start climbing up with a speed \(v\) relative to the string and the second with speed of 2 \(v\). Both monkeys have got same masses. The time taken by the first and second monkeys in reaching the pulleys are respectively.
363069 A massless string of length \(l\) passes over a frictionless pulley with horizontal axis. Two monkeys hang from the ends of the string at the distance \(l\)/2 from the pulley, a monkey start climbing up with a speed \(v\) relative to the string and the second with speed of 2 \(v\). Both monkeys have got same masses. The time taken by the first and second monkeys in reaching the pulleys are respectively.