363127
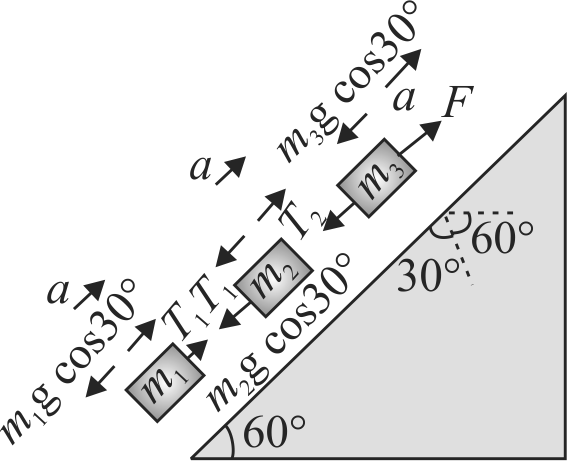
Three blocks of mass \(m_{1}=2.0, m_{2}=4.0\) and \(m_{3}=6.0 \mathrm{~kg}\) are connected by strings on a frictionless inclined plane of \(60^{\circ}\), as shown in the figure. A force \(F = 120\;N\) is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The value of tension \(T_{1}\) and \(T_{2}\) in the cords are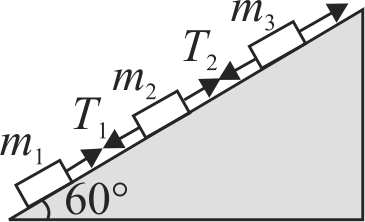
363129
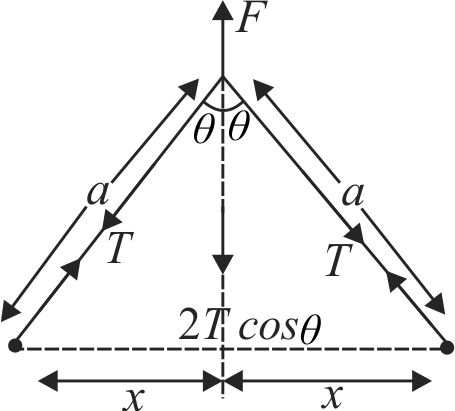
Two particles of mass \(m\) each are tied at the ends of a light string of length 2 \(a\). The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance ‘\(a\)’ from the centre \(P\) (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force \(F\). As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2 \(x\), is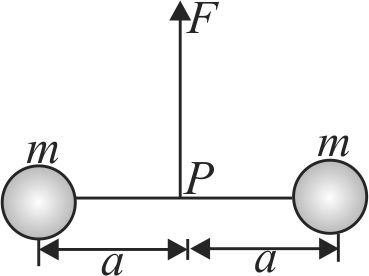
363127
Three blocks of mass \(m_{1}=2.0, m_{2}=4.0\) and \(m_{3}=6.0 \mathrm{~kg}\) are connected by strings on a frictionless inclined plane of \(60^{\circ}\), as shown in the figure. A force \(F = 120\;N\) is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The value of tension \(T_{1}\) and \(T_{2}\) in the cords are
363129
Two particles of mass \(m\) each are tied at the ends of a light string of length 2 \(a\). The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance ‘\(a\)’ from the centre \(P\) (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force \(F\). As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2 \(x\), is
363127
Three blocks of mass \(m_{1}=2.0, m_{2}=4.0\) and \(m_{3}=6.0 \mathrm{~kg}\) are connected by strings on a frictionless inclined plane of \(60^{\circ}\), as shown in the figure. A force \(F = 120\;N\) is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The value of tension \(T_{1}\) and \(T_{2}\) in the cords are
363129
Two particles of mass \(m\) each are tied at the ends of a light string of length 2 \(a\). The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance ‘\(a\)’ from the centre \(P\) (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force \(F\). As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2 \(x\), is
363127
Three blocks of mass \(m_{1}=2.0, m_{2}=4.0\) and \(m_{3}=6.0 \mathrm{~kg}\) are connected by strings on a frictionless inclined plane of \(60^{\circ}\), as shown in the figure. A force \(F = 120\;N\) is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The value of tension \(T_{1}\) and \(T_{2}\) in the cords are
363129
Two particles of mass \(m\) each are tied at the ends of a light string of length 2 \(a\). The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance ‘\(a\)’ from the centre \(P\) (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force \(F\). As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2 \(x\), is
363127
Three blocks of mass \(m_{1}=2.0, m_{2}=4.0\) and \(m_{3}=6.0 \mathrm{~kg}\) are connected by strings on a frictionless inclined plane of \(60^{\circ}\), as shown in the figure. A force \(F = 120\;N\) is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The value of tension \(T_{1}\) and \(T_{2}\) in the cords are
363129
Two particles of mass \(m\) each are tied at the ends of a light string of length 2 \(a\). The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance ‘\(a\)’ from the centre \(P\) (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force \(F\). As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2 \(x\), is

.png)