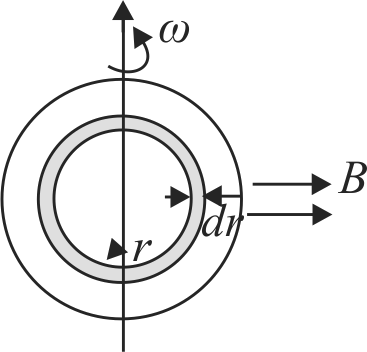
363045 A dielectric disc of radius \(R\) carries a charge uniformly on its surface. The surface charge density is \(\sigma\). The disc rotates about an axis perpendicular to its plane passing through the centre with angular velocity \(\omega\). Find the torque on the disc if it is placed in a uniform magnetic field \(b\) directed perpendicular to the rotation axis.

363046 The torque required to hold a small circular coil of 10 turns, area \(1\;m{m^2}\) and carrying a current of (21/44) A in the middle of a long solenoid of \({10^3}\) turns/ \(m\) carrying a current of 2.5\(A\) with its axis perpendicular to the axis of the solenoid is:

363047 A conducting ring of mass 2\(kg\) and radius 0.5\(m\) is placed on a smooth horizontal plane. The ring carries a current of \(I = 4\;A\). A horizontal magnetic field \(B = 10\;T\) is switched on a time \(t = 0\) as shown in figure. The initial angular acceleration of the ring will be: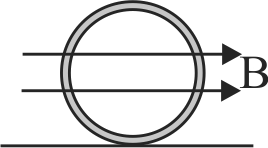

363048 As shown in the figure, three sided frame is pivoted at \({P}\) and \({Q}\) hangs vertically. Its sides are of same length and have a linear density of \({\sqrt{3} {~kg} / {m}}\). A current of \({10 \sqrt{3} {~A}}\) is sent through the frame, which is in a uniform magnetic field of \(2\,T\) directed upwards as shown in the figure. Then, angle through which the frame will be deflected in equilibrium is \({\dfrac{\pi}{k}}\). Find the value of \({k}\) is (Given, \({g=10 {~m} / {s}^{2}}\))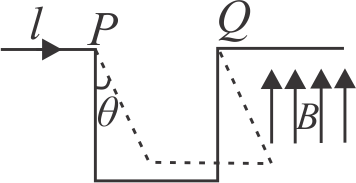

363045 A dielectric disc of radius \(R\) carries a charge uniformly on its surface. The surface charge density is \(\sigma\). The disc rotates about an axis perpendicular to its plane passing through the centre with angular velocity \(\omega\). Find the torque on the disc if it is placed in a uniform magnetic field \(b\) directed perpendicular to the rotation axis.

363046 The torque required to hold a small circular coil of 10 turns, area \(1\;m{m^2}\) and carrying a current of (21/44) A in the middle of a long solenoid of \({10^3}\) turns/ \(m\) carrying a current of 2.5\(A\) with its axis perpendicular to the axis of the solenoid is:

363047 A conducting ring of mass 2\(kg\) and radius 0.5\(m\) is placed on a smooth horizontal plane. The ring carries a current of \(I = 4\;A\). A horizontal magnetic field \(B = 10\;T\) is switched on a time \(t = 0\) as shown in figure. The initial angular acceleration of the ring will be:

363048 As shown in the figure, three sided frame is pivoted at \({P}\) and \({Q}\) hangs vertically. Its sides are of same length and have a linear density of \({\sqrt{3} {~kg} / {m}}\). A current of \({10 \sqrt{3} {~A}}\) is sent through the frame, which is in a uniform magnetic field of \(2\,T\) directed upwards as shown in the figure. Then, angle through which the frame will be deflected in equilibrium is \({\dfrac{\pi}{k}}\). Find the value of \({k}\) is (Given, \({g=10 {~m} / {s}^{2}}\))

363045 A dielectric disc of radius \(R\) carries a charge uniformly on its surface. The surface charge density is \(\sigma\). The disc rotates about an axis perpendicular to its plane passing through the centre with angular velocity \(\omega\). Find the torque on the disc if it is placed in a uniform magnetic field \(b\) directed perpendicular to the rotation axis.

363046 The torque required to hold a small circular coil of 10 turns, area \(1\;m{m^2}\) and carrying a current of (21/44) A in the middle of a long solenoid of \({10^3}\) turns/ \(m\) carrying a current of 2.5\(A\) with its axis perpendicular to the axis of the solenoid is:

363047 A conducting ring of mass 2\(kg\) and radius 0.5\(m\) is placed on a smooth horizontal plane. The ring carries a current of \(I = 4\;A\). A horizontal magnetic field \(B = 10\;T\) is switched on a time \(t = 0\) as shown in figure. The initial angular acceleration of the ring will be:

363048 As shown in the figure, three sided frame is pivoted at \({P}\) and \({Q}\) hangs vertically. Its sides are of same length and have a linear density of \({\sqrt{3} {~kg} / {m}}\). A current of \({10 \sqrt{3} {~A}}\) is sent through the frame, which is in a uniform magnetic field of \(2\,T\) directed upwards as shown in the figure. Then, angle through which the frame will be deflected in equilibrium is \({\dfrac{\pi}{k}}\). Find the value of \({k}\) is (Given, \({g=10 {~m} / {s}^{2}}\))

363045 A dielectric disc of radius \(R\) carries a charge uniformly on its surface. The surface charge density is \(\sigma\). The disc rotates about an axis perpendicular to its plane passing through the centre with angular velocity \(\omega\). Find the torque on the disc if it is placed in a uniform magnetic field \(b\) directed perpendicular to the rotation axis.

363046 The torque required to hold a small circular coil of 10 turns, area \(1\;m{m^2}\) and carrying a current of (21/44) A in the middle of a long solenoid of \({10^3}\) turns/ \(m\) carrying a current of 2.5\(A\) with its axis perpendicular to the axis of the solenoid is:

363047 A conducting ring of mass 2\(kg\) and radius 0.5\(m\) is placed on a smooth horizontal plane. The ring carries a current of \(I = 4\;A\). A horizontal magnetic field \(B = 10\;T\) is switched on a time \(t = 0\) as shown in figure. The initial angular acceleration of the ring will be:

363048 As shown in the figure, three sided frame is pivoted at \({P}\) and \({Q}\) hangs vertically. Its sides are of same length and have a linear density of \({\sqrt{3} {~kg} / {m}}\). A current of \({10 \sqrt{3} {~A}}\) is sent through the frame, which is in a uniform magnetic field of \(2\,T\) directed upwards as shown in the figure. Then, angle through which the frame will be deflected in equilibrium is \({\dfrac{\pi}{k}}\). Find the value of \({k}\) is (Given, \({g=10 {~m} / {s}^{2}}\))