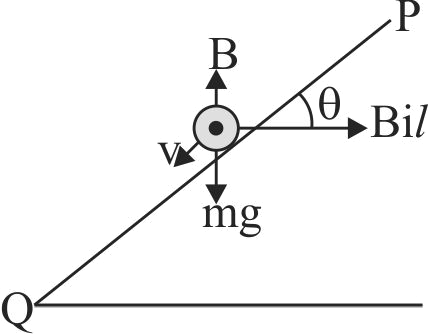
362767 A conductor rod of a length \(l\) and mass \(m\) is moving down a smooth inclined plane of inclination \(\theta\) with constant speed \(\mathrm{v}\). The current is flowing through the rod into the page. The required magnetic field in vertically upward direction to maintain constant speed for the rod is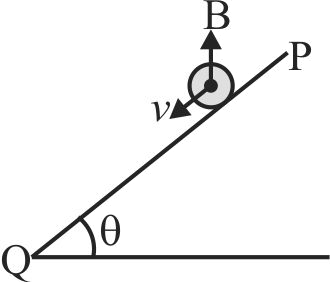

362768 A conductor \(ABCDE\), shaped as shown, carries current \(I\). It is placed in the \(x-y\) plane with the ends \(A\) and \(E\) on the \(x\)-axis. A uniform magnetic field of magnitude \(B\) exists in the region. Predict the wrong option for the force on the wire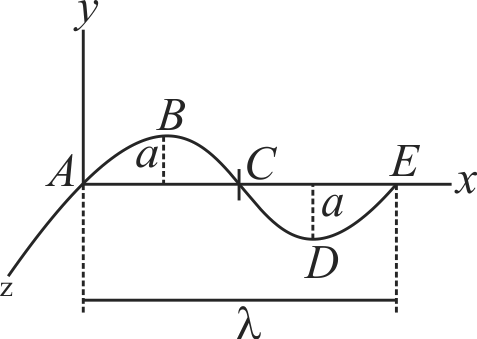

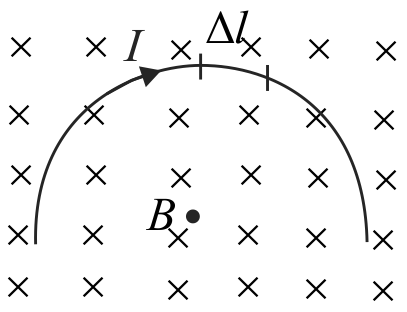
362769 A semicircular ring (carrying a current \(I\) ) is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring.
Assertion :
Force \(\vec{F}\) on each element of ring is different.
Reason :
Net force on ring must be perpendicular to magnetic field.

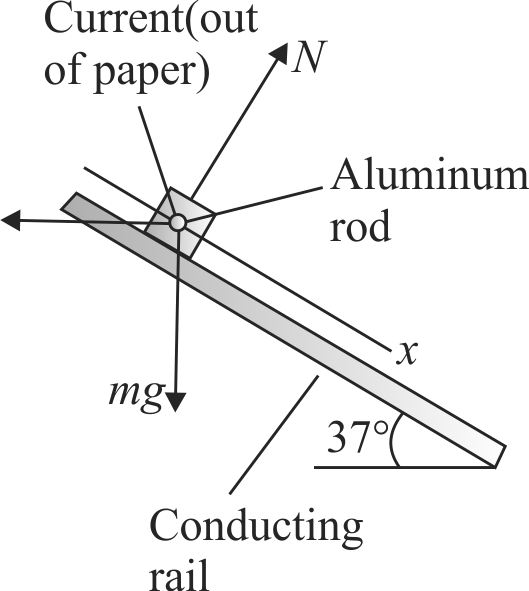
362770 The two conducting rails in the drawing are tilted upward so they each make an angle of \({37^{\circ}}\) with respect to the ground. The vertical magnetic field has a magnitude of 0.050 \(T\) . The \({0.20-{kg}}\) aluminium rod (length \({=2.0 {~m}}\) ) slides without friction down the rails at a constant velocity. How much current flows through the rod ?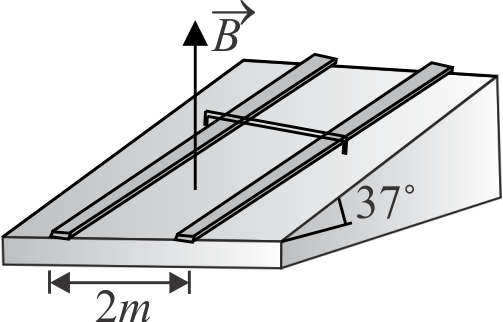

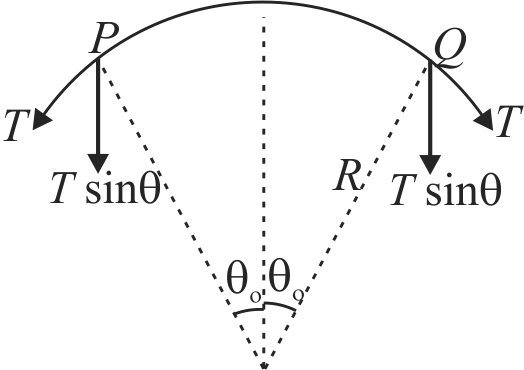
362771 A wire carrying current \(I\) is tied between points \(P\) and \(Q\) and is in the shape of a circular are of radius \(R\) due to a uniform magnetic field \(B\) (perpendicular to the plane of the paper, shown) in the vicinity of the wire. If the wire subtends an angle \(2 \theta_{0}\) at the centre of the circle (of which it forms an arc) then the tension in the wire is :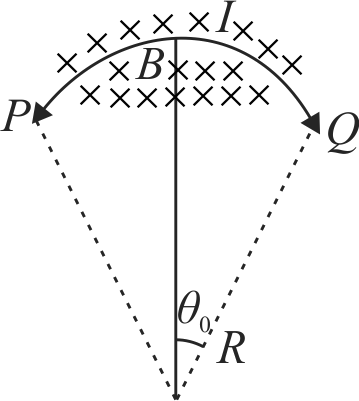

362767 A conductor rod of a length \(l\) and mass \(m\) is moving down a smooth inclined plane of inclination \(\theta\) with constant speed \(\mathrm{v}\). The current is flowing through the rod into the page. The required magnetic field in vertically upward direction to maintain constant speed for the rod is

362768 A conductor \(ABCDE\), shaped as shown, carries current \(I\). It is placed in the \(x-y\) plane with the ends \(A\) and \(E\) on the \(x\)-axis. A uniform magnetic field of magnitude \(B\) exists in the region. Predict the wrong option for the force on the wire

362769 A semicircular ring (carrying a current \(I\) ) is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring.
Assertion :
Force \(\vec{F}\) on each element of ring is different.
Reason :
Net force on ring must be perpendicular to magnetic field.

362770 The two conducting rails in the drawing are tilted upward so they each make an angle of \({37^{\circ}}\) with respect to the ground. The vertical magnetic field has a magnitude of 0.050 \(T\) . The \({0.20-{kg}}\) aluminium rod (length \({=2.0 {~m}}\) ) slides without friction down the rails at a constant velocity. How much current flows through the rod ?

362771 A wire carrying current \(I\) is tied between points \(P\) and \(Q\) and is in the shape of a circular are of radius \(R\) due to a uniform magnetic field \(B\) (perpendicular to the plane of the paper, shown) in the vicinity of the wire. If the wire subtends an angle \(2 \theta_{0}\) at the centre of the circle (of which it forms an arc) then the tension in the wire is :

362767 A conductor rod of a length \(l\) and mass \(m\) is moving down a smooth inclined plane of inclination \(\theta\) with constant speed \(\mathrm{v}\). The current is flowing through the rod into the page. The required magnetic field in vertically upward direction to maintain constant speed for the rod is

362768 A conductor \(ABCDE\), shaped as shown, carries current \(I\). It is placed in the \(x-y\) plane with the ends \(A\) and \(E\) on the \(x\)-axis. A uniform magnetic field of magnitude \(B\) exists in the region. Predict the wrong option for the force on the wire

362769 A semicircular ring (carrying a current \(I\) ) is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring.
Assertion :
Force \(\vec{F}\) on each element of ring is different.
Reason :
Net force on ring must be perpendicular to magnetic field.

362770 The two conducting rails in the drawing are tilted upward so they each make an angle of \({37^{\circ}}\) with respect to the ground. The vertical magnetic field has a magnitude of 0.050 \(T\) . The \({0.20-{kg}}\) aluminium rod (length \({=2.0 {~m}}\) ) slides without friction down the rails at a constant velocity. How much current flows through the rod ?

362771 A wire carrying current \(I\) is tied between points \(P\) and \(Q\) and is in the shape of a circular are of radius \(R\) due to a uniform magnetic field \(B\) (perpendicular to the plane of the paper, shown) in the vicinity of the wire. If the wire subtends an angle \(2 \theta_{0}\) at the centre of the circle (of which it forms an arc) then the tension in the wire is :

362767 A conductor rod of a length \(l\) and mass \(m\) is moving down a smooth inclined plane of inclination \(\theta\) with constant speed \(\mathrm{v}\). The current is flowing through the rod into the page. The required magnetic field in vertically upward direction to maintain constant speed for the rod is

362768 A conductor \(ABCDE\), shaped as shown, carries current \(I\). It is placed in the \(x-y\) plane with the ends \(A\) and \(E\) on the \(x\)-axis. A uniform magnetic field of magnitude \(B\) exists in the region. Predict the wrong option for the force on the wire

362769 A semicircular ring (carrying a current \(I\) ) is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring.
Assertion :
Force \(\vec{F}\) on each element of ring is different.
Reason :
Net force on ring must be perpendicular to magnetic field.

362770 The two conducting rails in the drawing are tilted upward so they each make an angle of \({37^{\circ}}\) with respect to the ground. The vertical magnetic field has a magnitude of 0.050 \(T\) . The \({0.20-{kg}}\) aluminium rod (length \({=2.0 {~m}}\) ) slides without friction down the rails at a constant velocity. How much current flows through the rod ?

362771 A wire carrying current \(I\) is tied between points \(P\) and \(Q\) and is in the shape of a circular are of radius \(R\) due to a uniform magnetic field \(B\) (perpendicular to the plane of the paper, shown) in the vicinity of the wire. If the wire subtends an angle \(2 \theta_{0}\) at the centre of the circle (of which it forms an arc) then the tension in the wire is :

362767 A conductor rod of a length \(l\) and mass \(m\) is moving down a smooth inclined plane of inclination \(\theta\) with constant speed \(\mathrm{v}\). The current is flowing through the rod into the page. The required magnetic field in vertically upward direction to maintain constant speed for the rod is

362768 A conductor \(ABCDE\), shaped as shown, carries current \(I\). It is placed in the \(x-y\) plane with the ends \(A\) and \(E\) on the \(x\)-axis. A uniform magnetic field of magnitude \(B\) exists in the region. Predict the wrong option for the force on the wire

362769 A semicircular ring (carrying a current \(I\) ) is present in the uniform magnetic field. Magnetic field is perpendicular to loop of ring.
Assertion :
Force \(\vec{F}\) on each element of ring is different.
Reason :
Net force on ring must be perpendicular to magnetic field.

362770 The two conducting rails in the drawing are tilted upward so they each make an angle of \({37^{\circ}}\) with respect to the ground. The vertical magnetic field has a magnitude of 0.050 \(T\) . The \({0.20-{kg}}\) aluminium rod (length \({=2.0 {~m}}\) ) slides without friction down the rails at a constant velocity. How much current flows through the rod ?

362771 A wire carrying current \(I\) is tied between points \(P\) and \(Q\) and is in the shape of a circular are of radius \(R\) due to a uniform magnetic field \(B\) (perpendicular to the plane of the paper, shown) in the vicinity of the wire. If the wire subtends an angle \(2 \theta_{0}\) at the centre of the circle (of which it forms an arc) then the tension in the wire is :