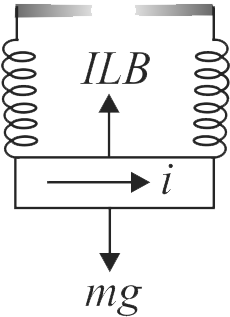
362750 A massless square loop, of wire of resistance \(10 \Omega\), supporting a mass of \(1 g\), hangs vertically with one of its sides in a uniform magnetic field of \({10^3}G\), directed outwards in the shaded region. A \(d c\) voltage \(V\) is applied to the loop. For what value of \(V\), the magnetic force will exactly balance the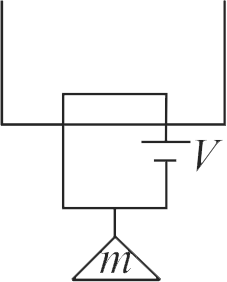

weight of the supporting mass of \(1\,g\)? (if sides
of the loop \(10\,cm,\,g = 10\,m{s^2}\))

362751 A wire carrying a current \(I\) along the positive \(x - \)axis has length \(L\). It is kept in a magnetic field \(\vec{B}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) T\). The magnitude of the magnetic force acting on the wire is:

362752 A wire \(P Q R S\) carrying a current runs along three edges of a cube of side \(l\) as shown. There exists a uniform magnetic field of magnitude \(B\) along one of the sides of the cube. The magnitude of the force acting on the wire is

362753 A current of \(10\;A\) is flowing in a wire of length \(1.5\;m\). A force of \(15\;N\) acts on it when it is placed in a uniform magnetic field of \(2\;T\). The angle between the magnetic field and the direction of the current is

362750 A massless square loop, of wire of resistance \(10 \Omega\), supporting a mass of \(1 g\), hangs vertically with one of its sides in a uniform magnetic field of \({10^3}G\), directed outwards in the shaded region. A \(d c\) voltage \(V\) is applied to the loop. For what value of \(V\), the magnetic force will exactly balance the

weight of the supporting mass of \(1\,g\)? (if sides
of the loop \(10\,cm,\,g = 10\,m{s^2}\))

362751 A wire carrying a current \(I\) along the positive \(x - \)axis has length \(L\). It is kept in a magnetic field \(\vec{B}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) T\). The magnitude of the magnetic force acting on the wire is:

362752 A wire \(P Q R S\) carrying a current runs along three edges of a cube of side \(l\) as shown. There exists a uniform magnetic field of magnitude \(B\) along one of the sides of the cube. The magnitude of the force acting on the wire is

362753 A current of \(10\;A\) is flowing in a wire of length \(1.5\;m\). A force of \(15\;N\) acts on it when it is placed in a uniform magnetic field of \(2\;T\). The angle between the magnetic field and the direction of the current is

362750 A massless square loop, of wire of resistance \(10 \Omega\), supporting a mass of \(1 g\), hangs vertically with one of its sides in a uniform magnetic field of \({10^3}G\), directed outwards in the shaded region. A \(d c\) voltage \(V\) is applied to the loop. For what value of \(V\), the magnetic force will exactly balance the

weight of the supporting mass of \(1\,g\)? (if sides
of the loop \(10\,cm,\,g = 10\,m{s^2}\))

362751 A wire carrying a current \(I\) along the positive \(x - \)axis has length \(L\). It is kept in a magnetic field \(\vec{B}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) T\). The magnitude of the magnetic force acting on the wire is:

362752 A wire \(P Q R S\) carrying a current runs along three edges of a cube of side \(l\) as shown. There exists a uniform magnetic field of magnitude \(B\) along one of the sides of the cube. The magnitude of the force acting on the wire is

362753 A current of \(10\;A\) is flowing in a wire of length \(1.5\;m\). A force of \(15\;N\) acts on it when it is placed in a uniform magnetic field of \(2\;T\). The angle between the magnetic field and the direction of the current is

362750 A massless square loop, of wire of resistance \(10 \Omega\), supporting a mass of \(1 g\), hangs vertically with one of its sides in a uniform magnetic field of \({10^3}G\), directed outwards in the shaded region. A \(d c\) voltage \(V\) is applied to the loop. For what value of \(V\), the magnetic force will exactly balance the

weight of the supporting mass of \(1\,g\)? (if sides
of the loop \(10\,cm,\,g = 10\,m{s^2}\))

362751 A wire carrying a current \(I\) along the positive \(x - \)axis has length \(L\). It is kept in a magnetic field \(\vec{B}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) T\). The magnitude of the magnetic force acting on the wire is:

362752 A wire \(P Q R S\) carrying a current runs along three edges of a cube of side \(l\) as shown. There exists a uniform magnetic field of magnitude \(B\) along one of the sides of the cube. The magnitude of the force acting on the wire is

362753 A current of \(10\;A\) is flowing in a wire of length \(1.5\;m\). A force of \(15\;N\) acts on it when it is placed in a uniform magnetic field of \(2\;T\). The angle between the magnetic field and the direction of the current is