362738
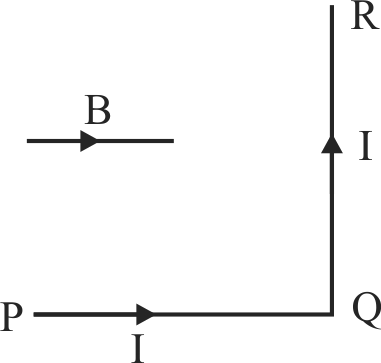
A wire \(PQ\) of mass 10\(g\) is at rest on two parallel metal rails. The separation between the rails is 4.9\(cm\). A magnetic field of 0.80 tesla is applied perpendicular to the plane of the rails. The resistance of the circuit is slowly decreases. When the resistance decreases to below \(20 \Omega\), the wire \(PQ\) begins to slide on the rails. Calculate the coefficient of friction between the wire and the rails.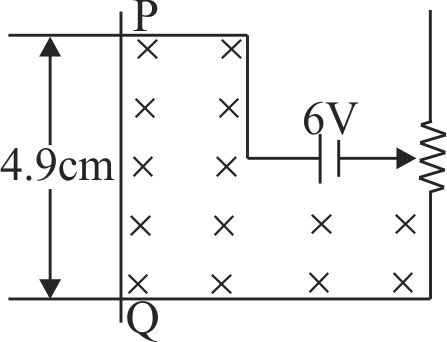
362741
A current of \(2\,A\) enters at the corner \({d}\) of a square frame \({a b c d}\) of side \(20\,cm\) and leaves at the opposite corner \({b}\). A magnetic field \({B=0.1 {~T}}\) exists in the space in a direction perpendicular to the plane of the frame as shown in the figure.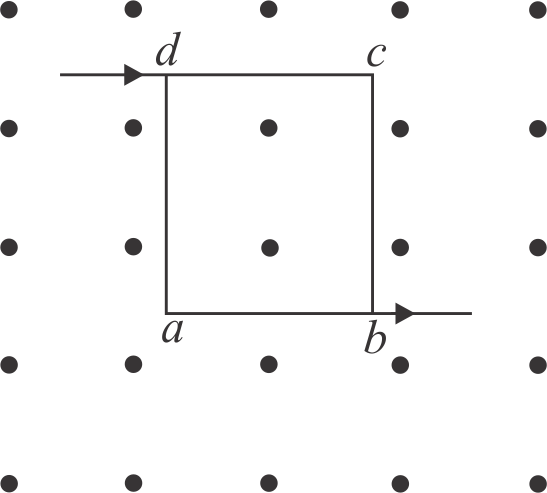
The magnitude of the magnetic forces on the four sides of the frame is \(x \times {10^{ - 2}}N.\) Find the value of \(x\) is
362738
A wire \(PQ\) of mass 10\(g\) is at rest on two parallel metal rails. The separation between the rails is 4.9\(cm\). A magnetic field of 0.80 tesla is applied perpendicular to the plane of the rails. The resistance of the circuit is slowly decreases. When the resistance decreases to below \(20 \Omega\), the wire \(PQ\) begins to slide on the rails. Calculate the coefficient of friction between the wire and the rails.
362741
A current of \(2\,A\) enters at the corner \({d}\) of a square frame \({a b c d}\) of side \(20\,cm\) and leaves at the opposite corner \({b}\). A magnetic field \({B=0.1 {~T}}\) exists in the space in a direction perpendicular to the plane of the frame as shown in the figure.
The magnitude of the magnetic forces on the four sides of the frame is \(x \times {10^{ - 2}}N.\) Find the value of \(x\) is
362738
A wire \(PQ\) of mass 10\(g\) is at rest on two parallel metal rails. The separation between the rails is 4.9\(cm\). A magnetic field of 0.80 tesla is applied perpendicular to the plane of the rails. The resistance of the circuit is slowly decreases. When the resistance decreases to below \(20 \Omega\), the wire \(PQ\) begins to slide on the rails. Calculate the coefficient of friction between the wire and the rails.
362741
A current of \(2\,A\) enters at the corner \({d}\) of a square frame \({a b c d}\) of side \(20\,cm\) and leaves at the opposite corner \({b}\). A magnetic field \({B=0.1 {~T}}\) exists in the space in a direction perpendicular to the plane of the frame as shown in the figure.
The magnitude of the magnetic forces on the four sides of the frame is \(x \times {10^{ - 2}}N.\) Find the value of \(x\) is
362738
A wire \(PQ\) of mass 10\(g\) is at rest on two parallel metal rails. The separation between the rails is 4.9\(cm\). A magnetic field of 0.80 tesla is applied perpendicular to the plane of the rails. The resistance of the circuit is slowly decreases. When the resistance decreases to below \(20 \Omega\), the wire \(PQ\) begins to slide on the rails. Calculate the coefficient of friction between the wire and the rails.
362741
A current of \(2\,A\) enters at the corner \({d}\) of a square frame \({a b c d}\) of side \(20\,cm\) and leaves at the opposite corner \({b}\). A magnetic field \({B=0.1 {~T}}\) exists in the space in a direction perpendicular to the plane of the frame as shown in the figure.
The magnitude of the magnetic forces on the four sides of the frame is \(x \times {10^{ - 2}}N.\) Find the value of \(x\) is
362738
A wire \(PQ\) of mass 10\(g\) is at rest on two parallel metal rails. The separation between the rails is 4.9\(cm\). A magnetic field of 0.80 tesla is applied perpendicular to the plane of the rails. The resistance of the circuit is slowly decreases. When the resistance decreases to below \(20 \Omega\), the wire \(PQ\) begins to slide on the rails. Calculate the coefficient of friction between the wire and the rails.
362741
A current of \(2\,A\) enters at the corner \({d}\) of a square frame \({a b c d}\) of side \(20\,cm\) and leaves at the opposite corner \({b}\). A magnetic field \({B=0.1 {~T}}\) exists in the space in a direction perpendicular to the plane of the frame as shown in the figure.
The magnitude of the magnetic forces on the four sides of the frame is \(x \times {10^{ - 2}}N.\) Find the value of \(x\) is