362689
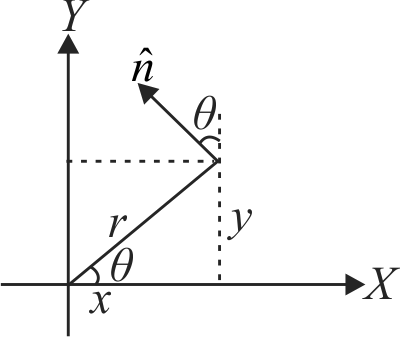
Figure shows an infinitely long wire carrying an outward current \({I_1}\). The current is along \(Z\) axis. There is a curved wire in \(x-y\) plane carrying current \(I_{2}\). The magnetic force on this wire between \(\left( {{x_1},{y_1}} \right)\)) and \(\left( {{x_2},{y_2}} \right)\) is: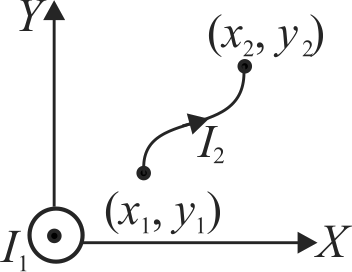
362689
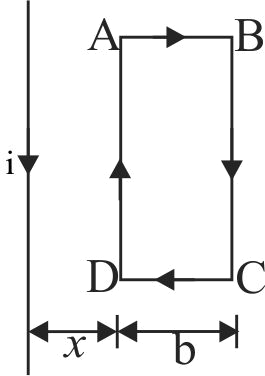
Figure shows an infinitely long wire carrying an outward current \({I_1}\). The current is along \(Z\) axis. There is a curved wire in \(x-y\) plane carrying current \(I_{2}\). The magnetic force on this wire between \(\left( {{x_1},{y_1}} \right)\)) and \(\left( {{x_2},{y_2}} \right)\) is:
362689
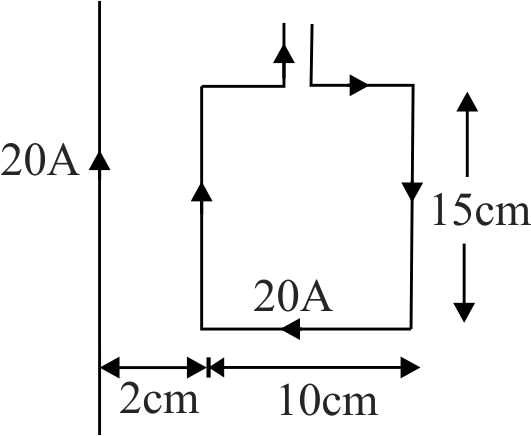
Figure shows an infinitely long wire carrying an outward current \({I_1}\). The current is along \(Z\) axis. There is a curved wire in \(x-y\) plane carrying current \(I_{2}\). The magnetic force on this wire between \(\left( {{x_1},{y_1}} \right)\)) and \(\left( {{x_2},{y_2}} \right)\) is:
362689
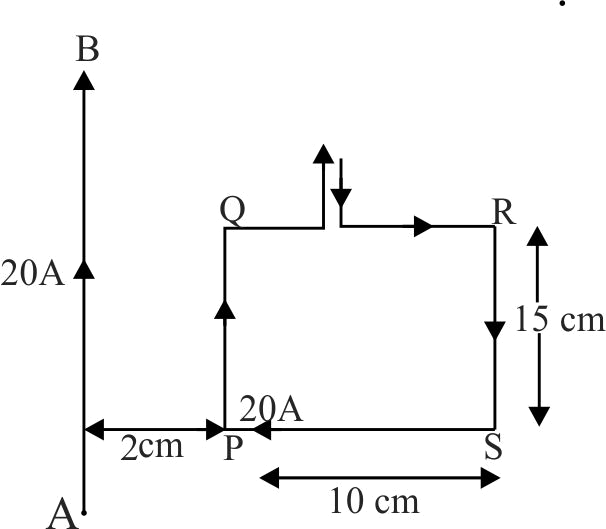
Figure shows an infinitely long wire carrying an outward current \({I_1}\). The current is along \(Z\) axis. There is a curved wire in \(x-y\) plane carrying current \(I_{2}\). The magnetic force on this wire between \(\left( {{x_1},{y_1}} \right)\)) and \(\left( {{x_2},{y_2}} \right)\) is:
362689
Figure shows an infinitely long wire carrying an outward current \({I_1}\). The current is along \(Z\) axis. There is a curved wire in \(x-y\) plane carrying current \(I_{2}\). The magnetic force on this wire between \(\left( {{x_1},{y_1}} \right)\)) and \(\left( {{x_2},{y_2}} \right)\) is: