362612
An equilateral triangle is made by uniform wires \(AB\), \(BC\), \(CA\). A current \(I\) enters at \(A\) and leaves from the mid point of \(BC\). If the lengths of each side of the triangle is \(L\). The magnetic field \(B\) at the centroid \(O\) of the triangle is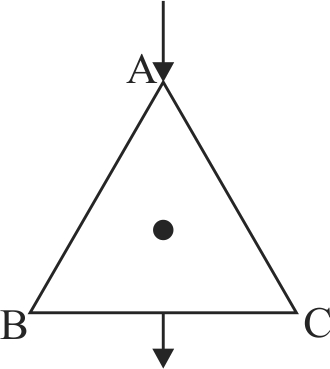
362612
An equilateral triangle is made by uniform wires \(AB\), \(BC\), \(CA\). A current \(I\) enters at \(A\) and leaves from the mid point of \(BC\). If the lengths of each side of the triangle is \(L\). The magnetic field \(B\) at the centroid \(O\) of the triangle is
362612
An equilateral triangle is made by uniform wires \(AB\), \(BC\), \(CA\). A current \(I\) enters at \(A\) and leaves from the mid point of \(BC\). If the lengths of each side of the triangle is \(L\). The magnetic field \(B\) at the centroid \(O\) of the triangle is
362612
An equilateral triangle is made by uniform wires \(AB\), \(BC\), \(CA\). A current \(I\) enters at \(A\) and leaves from the mid point of \(BC\). If the lengths of each side of the triangle is \(L\). The magnetic field \(B\) at the centroid \(O\) of the triangle is