Explanation:
Axis of the loop means a line passing through center of loop and normal to its plane. Since distance of the point \({P}\) is \({x}\) from center of loop and side of square loop is \({a}\) as shown in Figure. (a).
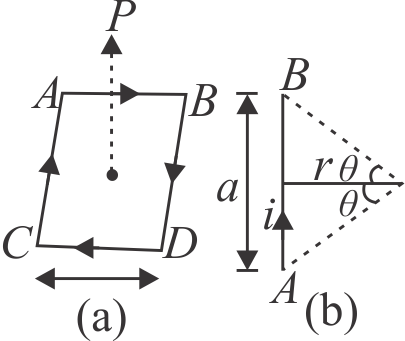
Therefore, perpendicular distance of \({P}\) from each side of
\(r=\sqrt{x^{2}+\left(\dfrac{a}{2}\right)^{2}}=4 {~cm}\)
Now, consider only one side \({A B}\) of the loop as shown in Figure. (b).
\(\begin{aligned}& \tan \alpha=\tan \beta=\dfrac{(a / 2)}{r}=\dfrac{3}{4} \\& \alpha=\beta=\tan ^{-1}\left(\dfrac{3}{4}\right)=37^{\circ}\end{aligned}\)
Magnitude of magnetic induction at \({P}\), due to current in this side \({A B}\), is
\(B_{0}=\dfrac{\mu_{0} I}{4 \pi r}(\sin \alpha+\sin \beta)=3 \times 10^{-6} {~T}\)
Now, consider magnetic inductions, produced by currents in two opposite sides \({A B}\) and \({C D}\) as shown in Figure. (c).
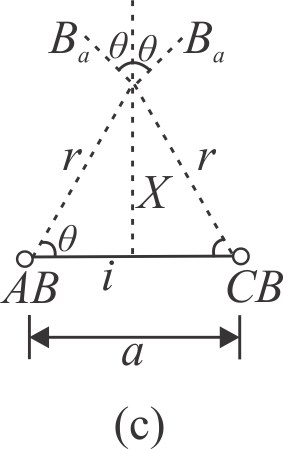
Components of these magnetic inductions, parallel to plane of loop neutralise each other. Hence, resultant of these two magnetic inductions is \({2 B_{0} \cos \theta}\) (along the axis).
Similarly, resultant of magnetic inductions produced by currents in remaining two opposite sides \({B C}\) and \({A D}\) will also be equal to \({2 B_{0} \cos \theta}\) (along the axis in same direction).
Hence, resultant magnetic induction,
\(B = 4{B_0}\cos \theta \)
\(B = 4 \times \left( {3 \times {{10}^{ - 6}}} \right)\frac{{(a/2)}}{r}\)
\( = 9 \times {10^{ - 6}}\;T = 9\,\mu T\)