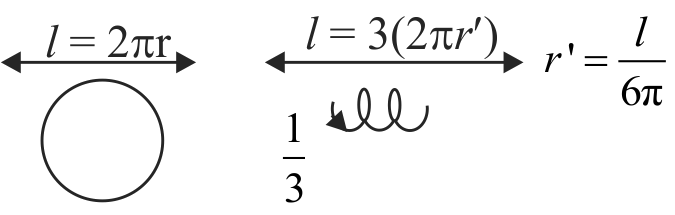362544
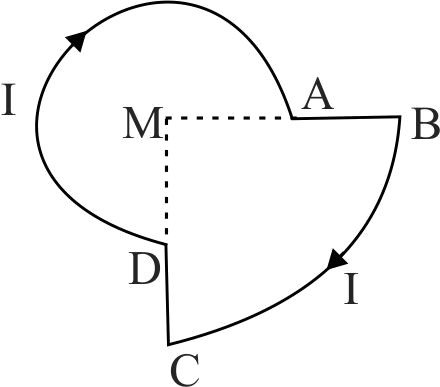
A current \(I\) is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is times \(\frac{{{\mu _0}{\text{I}}}}{{\text{R}}}\) times \((MA = R,MB = 2R,\angle DMA = 90^\circ )\)
362545 A certain length of insulated wire can be bent to form either a single circular loop (case I) or a double loop of smaller radius (case II). When the same steady current is passed through the wire, the ratio of the magnetic field at the centre in the case I to that in case II is:
362548 Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_{1}\) at its centre when a current (\(I\)) passes through it. The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field \({B_2}\) at the centre of the loops when current \(\frac{I}{3}\) passes through it. The ratio \({B_1}:{B_2}\):-
362544
A current \(I\) is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is times \(\frac{{{\mu _0}{\text{I}}}}{{\text{R}}}\) times \((MA = R,MB = 2R,\angle DMA = 90^\circ )\)
362545 A certain length of insulated wire can be bent to form either a single circular loop (case I) or a double loop of smaller radius (case II). When the same steady current is passed through the wire, the ratio of the magnetic field at the centre in the case I to that in case II is:
362548 Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_{1}\) at its centre when a current (\(I\)) passes through it. The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field \({B_2}\) at the centre of the loops when current \(\frac{I}{3}\) passes through it. The ratio \({B_1}:{B_2}\):-
362544
A current \(I\) is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is times \(\frac{{{\mu _0}{\text{I}}}}{{\text{R}}}\) times \((MA = R,MB = 2R,\angle DMA = 90^\circ )\)
362545 A certain length of insulated wire can be bent to form either a single circular loop (case I) or a double loop of smaller radius (case II). When the same steady current is passed through the wire, the ratio of the magnetic field at the centre in the case I to that in case II is:
362548 Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_{1}\) at its centre when a current (\(I\)) passes through it. The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field \({B_2}\) at the centre of the loops when current \(\frac{I}{3}\) passes through it. The ratio \({B_1}:{B_2}\):-
362544
A current \(I\) is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is times \(\frac{{{\mu _0}{\text{I}}}}{{\text{R}}}\) times \((MA = R,MB = 2R,\angle DMA = 90^\circ )\)
362545 A certain length of insulated wire can be bent to form either a single circular loop (case I) or a double loop of smaller radius (case II). When the same steady current is passed through the wire, the ratio of the magnetic field at the centre in the case I to that in case II is:
362548 Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_{1}\) at its centre when a current (\(I\)) passes through it. The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field \({B_2}\) at the centre of the loops when current \(\frac{I}{3}\) passes through it. The ratio \({B_1}:{B_2}\):-
362544
A current \(I\) is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is times \(\frac{{{\mu _0}{\text{I}}}}{{\text{R}}}\) times \((MA = R,MB = 2R,\angle DMA = 90^\circ )\)
362545 A certain length of insulated wire can be bent to form either a single circular loop (case I) or a double loop of smaller radius (case II). When the same steady current is passed through the wire, the ratio of the magnetic field at the centre in the case I to that in case II is:
362548 Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_{1}\) at its centre when a current (\(I\)) passes through it. The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field \({B_2}\) at the centre of the loops when current \(\frac{I}{3}\) passes through it. The ratio \({B_1}:{B_2}\):-